2020年版 ノルウェーメンサの答えと解説 Exercise 1〜35

この記事ではノルウェーメンサの答えの一覧と画像付きの解説を行なっています。
「解説はいいから答えだけ見たいよと言う方」は、目次をご覧ください。

Respect

• サイト名：IQ Test Made by Mensa Norway – Mensa Norway
• サイトURL：https://test.mensa.no/

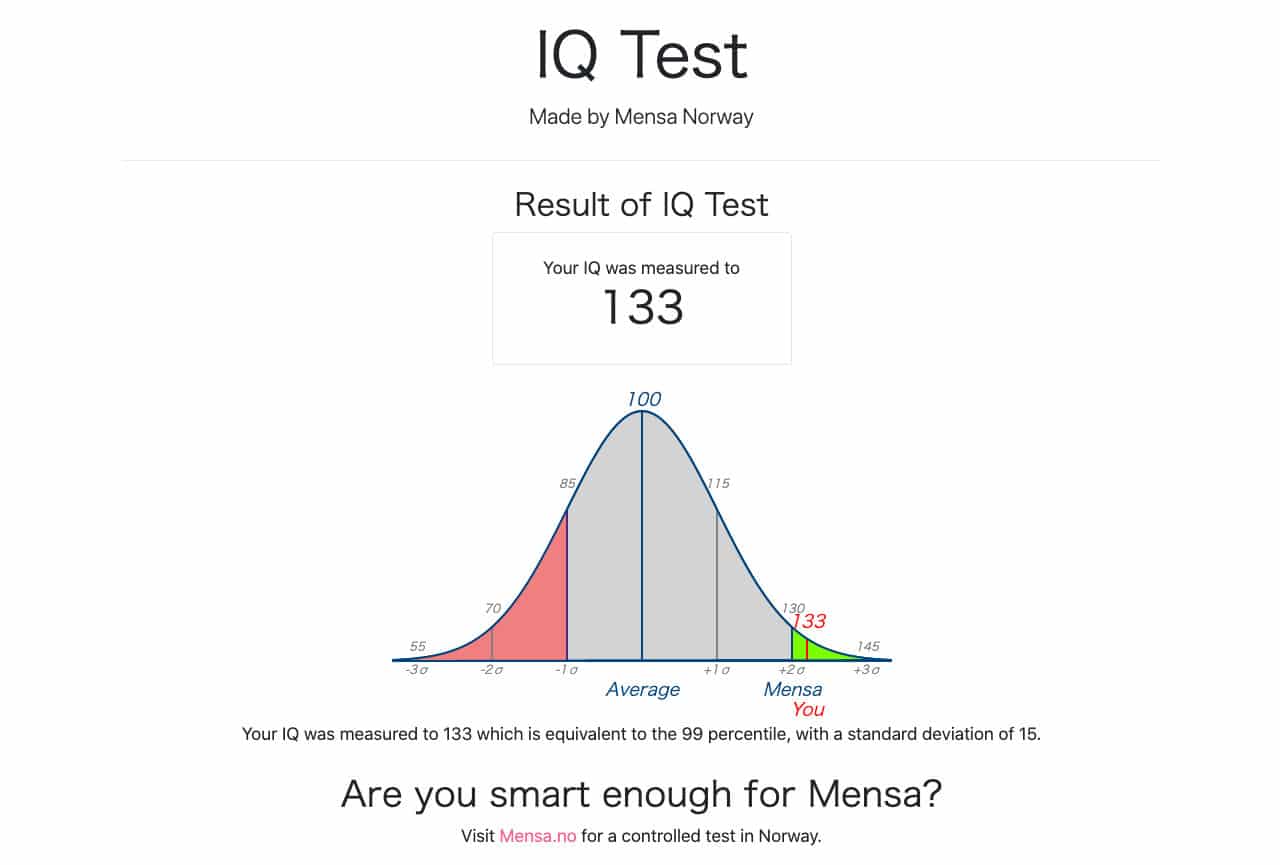
私の初回スコア

この記事を書いている私の初回スコアは133でした。初見ではExercise32. 33. 35. が時間切れで解けませんでした。かろうじて標準偏差15でパーセンタイル 99%なので、メンサ入会資格のIQ上位2%圏内にいるようです。参考になれば幸いです。

2020年版 ノルウェーメンサの答えと解説の一覧

IQテストの基本的な解き方。

1. 問題を上段、中段、下段に分けて考えます。
2. 上段から法則性を探します。
3. 上段で見つけた法則性を中段に適応し、見つけた法則性が正しいかを確認します。
4. 見つけた法則性が正しければ、法則性を下段に適応し、選択肢から正しいと思われる答えを選択します。
5. もし見つけた法則性が下段に適応できなかった場合、再度「手順2. 」から考えます。

*問題を解くにあたり、大抵もの問題は上中下段でグルーピングしてから、法則性を探す手順に入りますが、グルーピングが斜めになっているものや全ての図形の整合性から答えを導き出す問題もあり、決めつけないことも大切になります。

Exercise1.

問1の答え「A」

問1の解説

• IQテストの基本的な解き方に則って問題を解く。
• 黒マスが右へ１マスずつ移動している。

Exercise2.

問2の答え「E」

問2の解説

• IQテストの基本的な解き方に則って問題を解く。
• 外枠が同じ
• 中の記号が、「丸」→「十字」→「ひし形」の順に変化する。

Exercise3.

問3の答え「F」

問3の解説

• 外枠が同じ
• 中の記号が、「丸」→「十字」→「なし」に変化する。

Exercise4.

問4の答え「F」

問4の解説

• 黒色の長方形が棒の中を「右」→「真ん中」→「左」の順で移動する。

Exercise5.

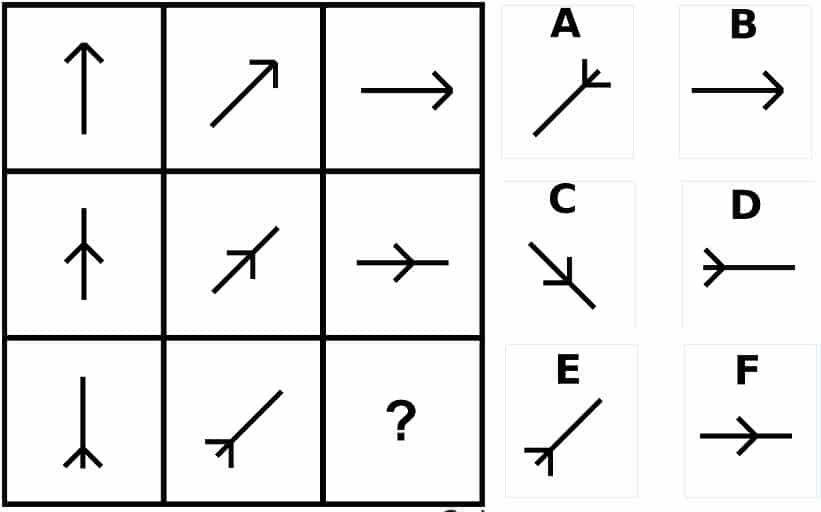
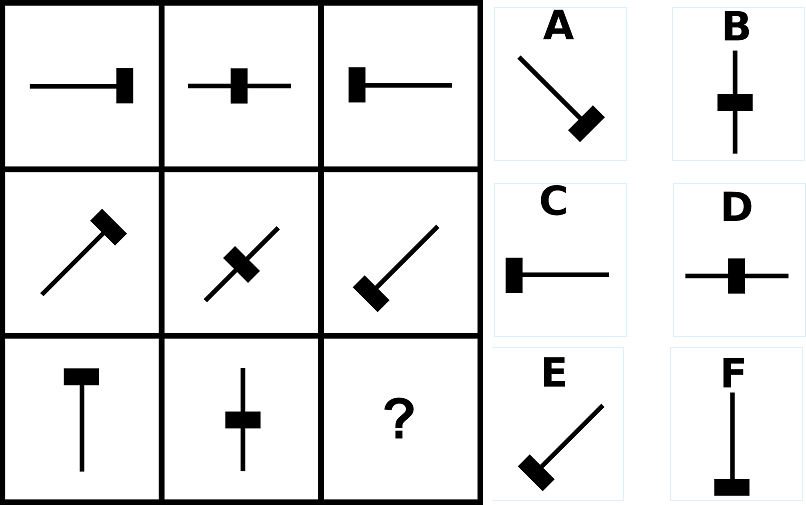
問5の答え「D」

問5の解説

• 棒が時計回りに45度ずつ回転する。

Exercise6.

問6の答え「E」

問6の解説

• 黒マスが一つずつ増える。

Exercise7.

問7の答え「E」

問7の解説

• 黒マスが一つずつ増える。
• 黒マスの開始地点が時計回りに90度ずつ回転する。

Exercise8.

問8の答え「C」

問8の解説

• 真ん中の黒点の数は5個で変化なし。
• 上側と下側の黒点の数はそれぞれ「1」「2」「3」個。

問8の解説2

• 上側の黒点の数をそれぞれ足すと「6」になる。
• 真ん中の黒点の数は「5」個。
• 下側の黒点の数をそれぞれ足すと「6」になる。

Exercise9.

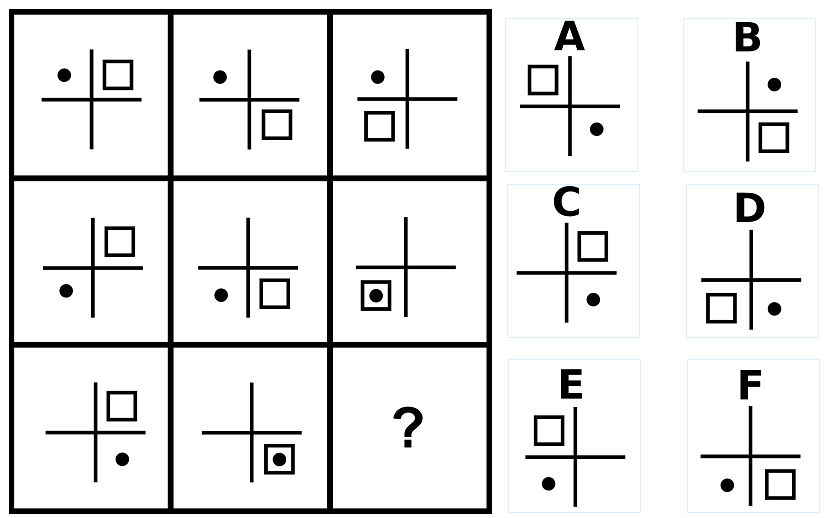
問9の答え「D」

問9の解説

• 黒点の位置は固定。
• 正方形が時計回りに90度ずつ回転する。

問9の解説2

• 黒点の位置は固定。
• 正方形が時計回りに1マスずつ移動する。

Exercise10.

問10の答え「D」

問10の解説

• 矢印の向きが反時計回りに90度ずつ回転する。
• 矢印の先を頂点とすると、矢印の左側が黒色。
• 矢印の先を頂点とすると、矢印の右側が白色。

Exercise11.

問11の答え「A」

問11の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した線^*2を消すと、右側の図形になる。

*2: 重複した線、重複した点、重複した部分。重ね合わさった線、重ね合わさった点、重ね合わさった部分、、、

Exercise12.

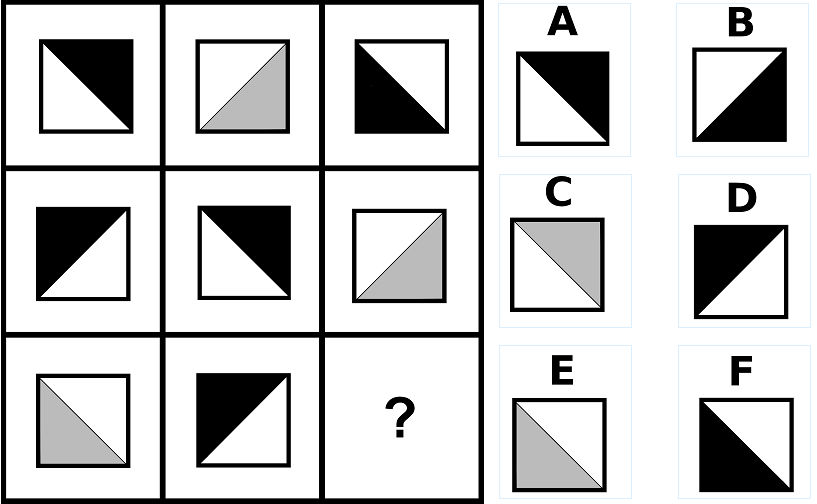
問12の答え「A」

問12の解説

• 図形が時計回りに90度ずつ回転する。
• 対角線で区切られた半分側の白色。
• 対角線で区切られた半分側の色が「黒」「黒」「灰」の順序で並ぶ。

問12の解説2

• 図形が時計回りに90度ずつ回転する。
• 対角線で区切られた半分側の白色。
• 対角線で区切られた半分側の色を数えると、「黒」2個、「灰」1個になる。

Exercise13.

問13の答え「B」

問13の解説

• 記号の中の色が「黒」→「白」→「灰」の順に変化する。
• 記号の形が「◯」→「△」→「□」の順に変化する。

Exercise14.

問14の答え「A」

問14の解説

• 棒線が「斜め」→「横」→「縦」の順に変化する。
• 記号の形が「◯」→「△」→「□」の順に変化する。

Exercise15.

問15の答え「F」

問15の解説

• 外枠が時計回りに90度ずつ回転する。
• 黒点の数が「3」→「2」→「1」と減る。

問15の解説2

• 外枠が時計回りに90度ずつ回転する。
• 黒点の数が「1」→「2」→「3」と増える。

問15の解説3

• 外枠が時計回りに90度ずつ回転する。
• 黒点の数は合わせて「6」個。

Exercise16.

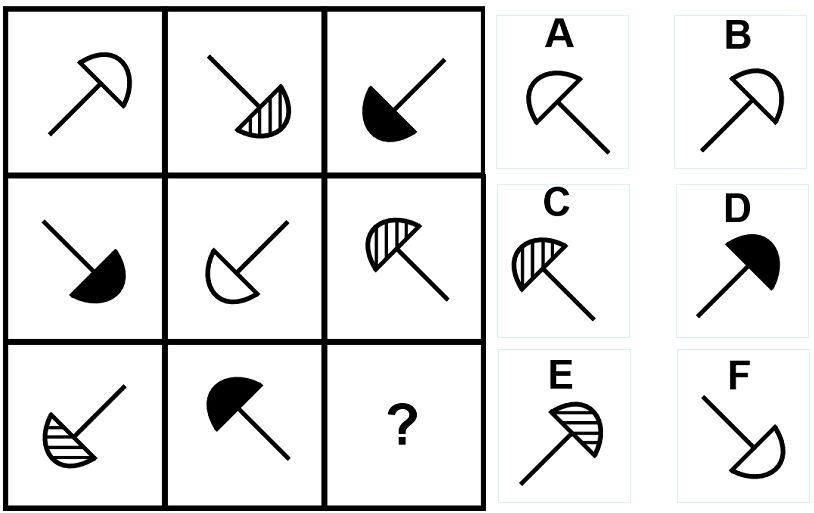
問16の答え「B」

問16の解説

• 棒線が時計回りに90度ずつ回転する。
• 傘の部分^*3の色が「白」→「灰」→「黒」の順に変化する。

*3: 傘の部分：頭、ピン、半円、、、様々な呼び名がある。🤔 

Exercise17.

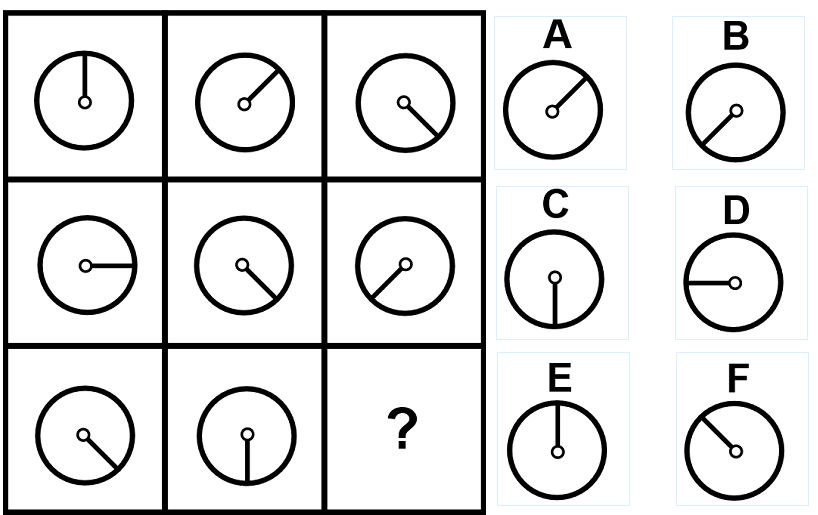
問17の答え「D」

問17の解説

• 時計の針が時計回りに「45度」→「90度」の順で回転する。

Exercise18.

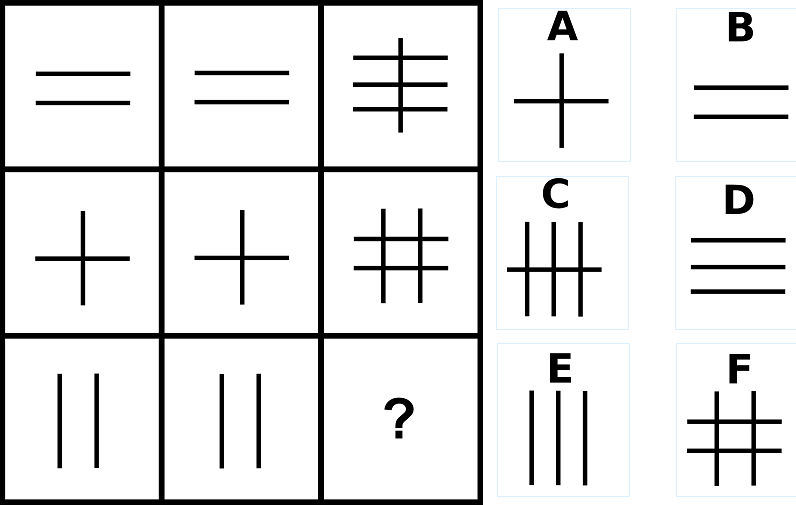
問18の答え「C」

問18の解説1

• 左側の棒線の数と真ん中の棒線の数を足す^*4と右側の棒線の数になる。
• 記号の向きは、「上段横向き」「中段十字」「下段縦向き」になる。

私は最初、「左側の棒線の数と真ん中の棒線の数を足す^*4と右側の棒線の数になる」だと思い、「F」と回答した。しかし不正解だった。この法則だと、選択肢は「C」と「F」となる。早とちりで選択してしまった。もう一つの法則性である「向き」を見落としていた。
*4: 棒線の数を足す：日本では数を数えるときに「正」の字を使うが、海外では「皿」か「爪」みたいな字や「☑︎」のような字を使う。このような線を引くことによって数を表す方法を「画線法」（かくせんほう）と呼ぶ。

問18の解説2

• 上段の画像を時計回りに90度回転させると、下段の画像となる。

Exercise19.

問19の答え「A」

問19の解説

• 外枠が「四角」→「四点」→「十字」の順で変化する。
• 中の記号が「ひし形」→「丸」→「なし」の順で変化する。

Exercise20.

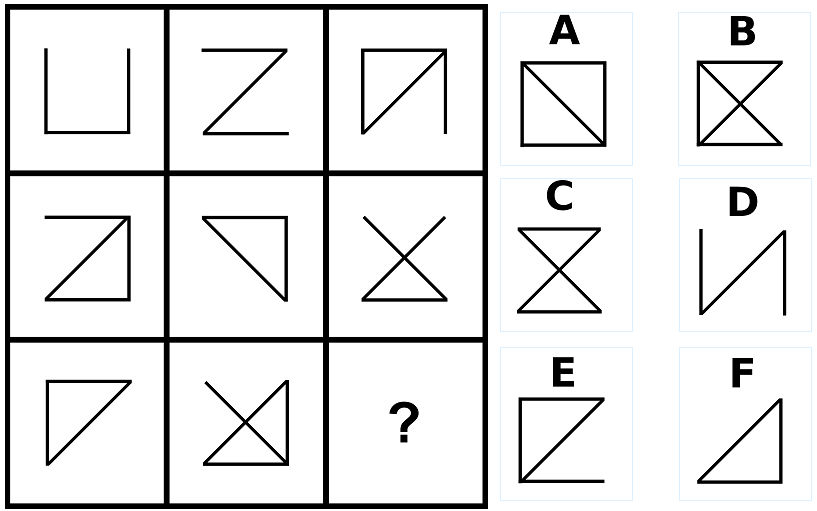
問20の答え「A」

問20の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した部分を消すと、右側の図形になる。

Exercise21.

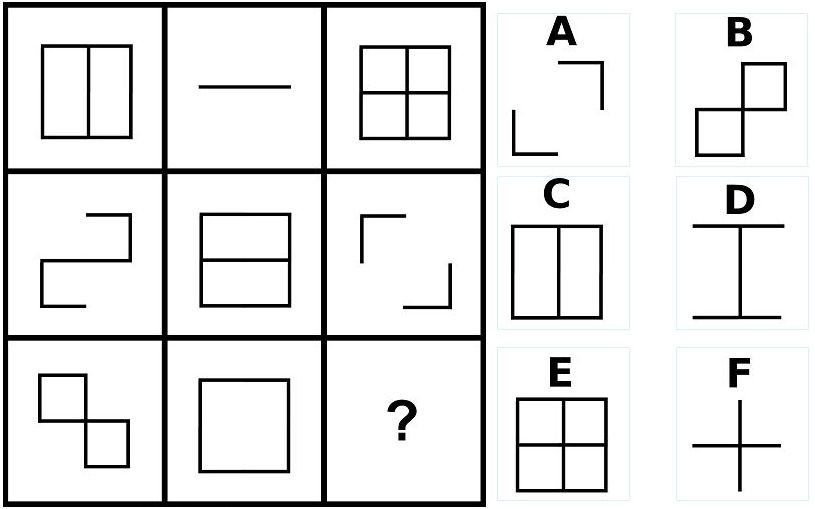
問21の答え「B」

問21の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した部分を消すと、右側の図形になる。

Exercise22.

問22の答え「E」

問22の解説

• 上側の記号は真ん中を境界に左右対象。
• 下側の記号は変化しない。

Exercise23.

問23の答え「F」

問23の解説

• 図形の種類は「■●△」「●□▲」「●△△」の3つ。
• 各図形は一段下がるごとに、中身の記号が1つずつ左に移動している。

*: 「●」を起点に考えると判り易い。

問23の解説2

• 図形の種類は「■●△」「●□▲」「●△△」の3つ。
• 各図形は一段下がるごとに、中身の記号が左方向に1マス スライドしている。

問23の解説2

• 組み分けを右上がり斜めで行う。 ↗ ↗ ↗
• 図形の種類は「■●△」「●□▲」「●△△」の3つ。
• 各図形は一段下がるごとに、中身の記号が左方向に1マス スライドしている。

Exercise24.

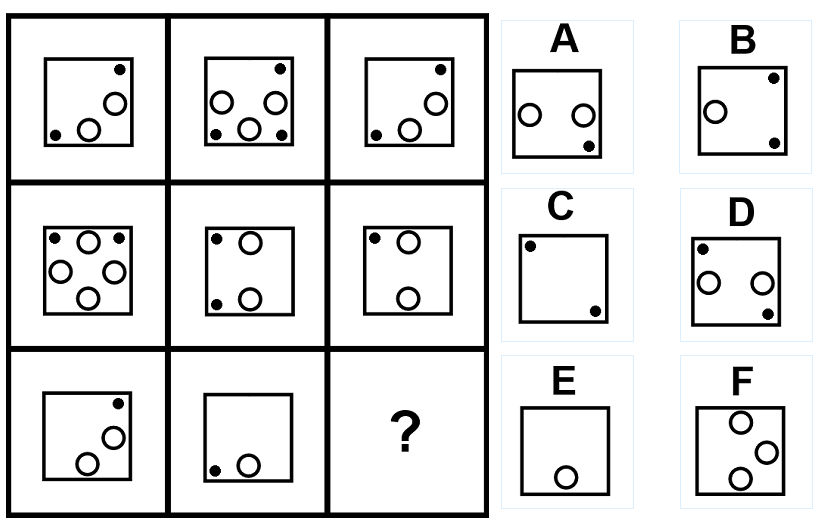
問24の答え「F」

問24の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した部分を消すと、右側の図形になる。

Exercise25.

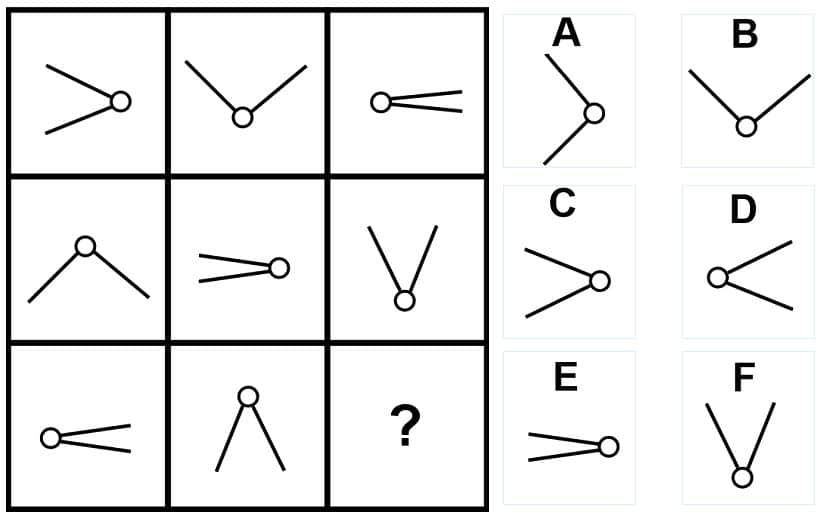
問25の答え「E」

問25の解説

• 左側の図形と真ん中の図形を重ね合わせると、右側の図形になる。
• 「・」と「・」が重なると「・」になる。
• 「◯」と「◯」が重なると「◯」になる。
• 重複しない記号は「なし」になる。

Exercise26.

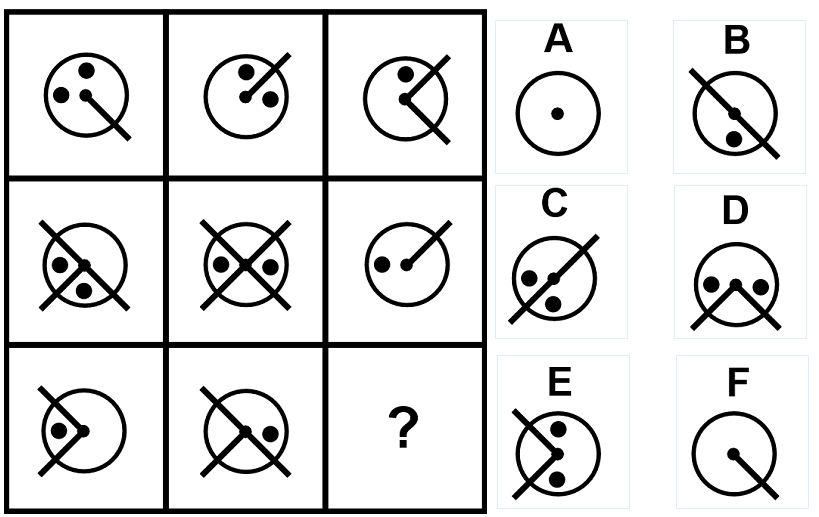
問26の答え「F」

問26の解説

• 左側の図形と真ん中の図形を重ね合わせると、右側の図形になる。
• 重複した「・」はそのまま。
• 重複しない「・」は消える。
• 重複した線は消える。
• 重複しない線はそのまま。

Exercise27.

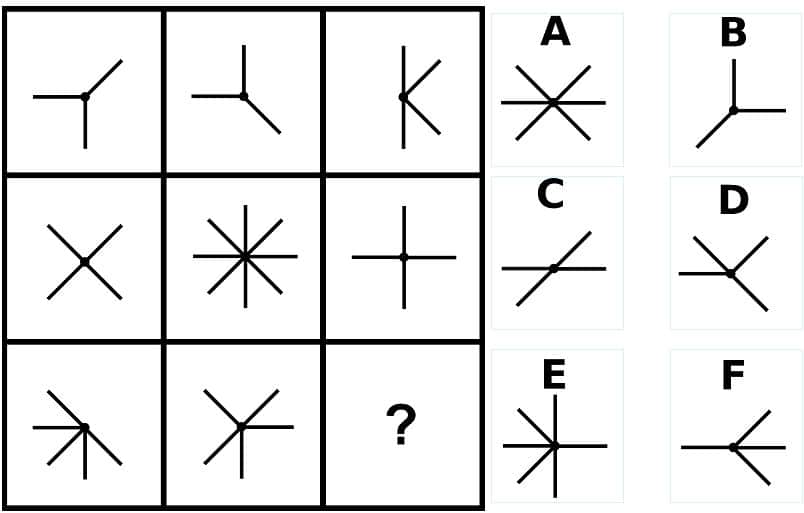
問27の答え「A」

問27の解説

• 記号が時計回りに90度ずつ回転している。
• 足の開きが「小」→「中」→「大」の順に変化する。

*: このような一般に馴染みのない記号は、脳内で操作する際に身近な物に置き換えると操作難易度が下がる。「安全ピン、ハサミ、トング、バネ」など。すでに脳内にその物を触った記憶と経験がある分、未知の記号でも既知の物と置き換えれば、既存の記憶と経験の脳回路が使える為。

Exercise28.

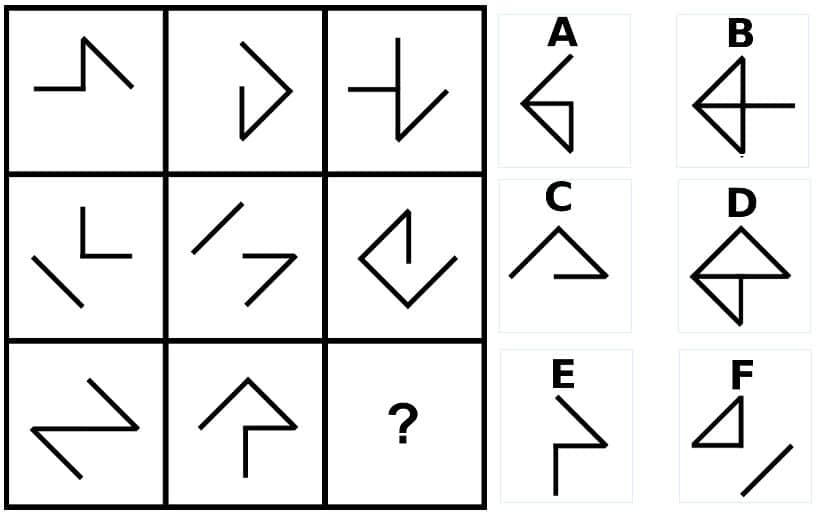
問28の答え「A」

問28の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した部分を消すと、右側の図形になる。

Exercise29.

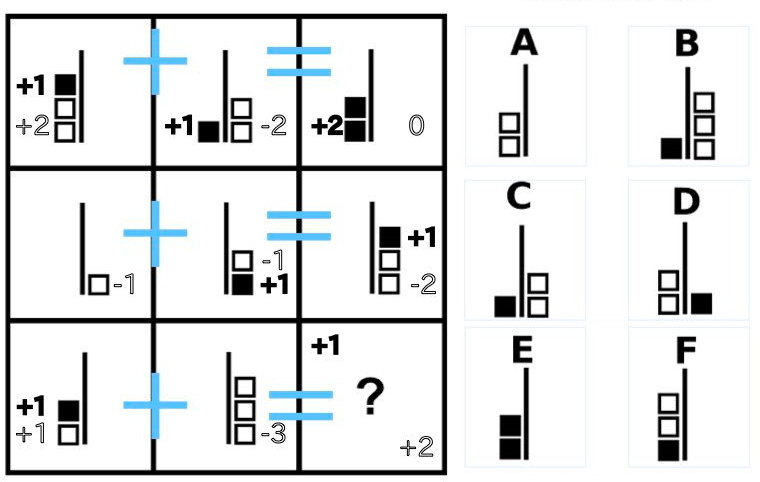
問29の答え「C」

問29の解説

• 左側と真ん中の各記号を足し算すると、右側の図形になる。
• 左側黒色：正の数
• 左側白色：正の数
• 右側黒色：正の数
• 右側白色：負の数

Exercise30.

問30の答え「E」

問30の解説

• 左側の図形と真ん中の図形を重ね、法則に従って変化させると右側の図形になる。
• 「●」＋「●」＝「□」（候補：A, E )
• 「　」＋「□」＝「□」（候補：B, E, F )
• 「□」＋「●」＝「　」
• 「●」＋「　」＝「●」（候補：A, C, E )
• 上記3つの法則性で共通している選択肢は「E」なので、答えは「E」

*:「□」＋「□」＝「???」 // このパターンの答えは不明だが、他の法則性を使用し、フィルタリングで答えは導き出せる。

*: 速解のコツとしては、脳内操作するときの言葉を上段の「黒点」＋「黒点」＝「四角」ならば、”黒黒白”と言語変換すると良い。余計な言葉(思考)を排除した言語変換で余計な脳内思考リソースを省いて省メモリーで脳内操作が可能になる為。「黒い点」よりも”黒”、「白い四角」よりも”白”と言語変換した方が良い。コンパクトな方が操作がし易いのは、閉じた一冊の本を片手で左から右へ動かすことよりも、開いた一冊の本を片手で左から右へ動かすのが難しいのを想像していただければ良い。

Exercise31.

問31の答え「D」

問31の解説

• 左側の図形と真ん中の図形を重ね合わせて、重複した部分を消すと、右側の図形になる。

Exercise32.

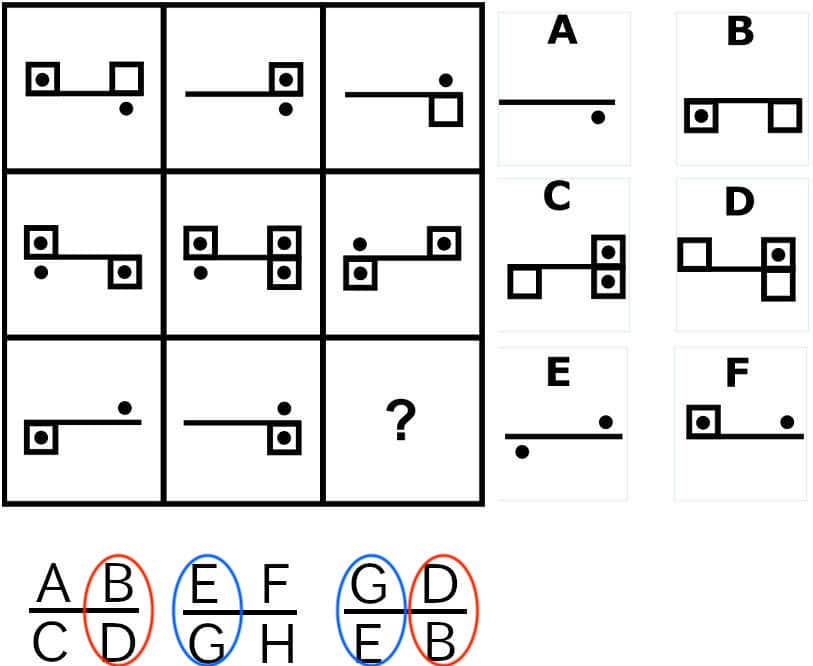
問32の答え「A」

問32の解説

• 左側の図形の右半分を上下反転した画像が、右側の図形の右半分になる。
• 真ん中の図形の左半分を上下反転した画像が、右側の図形の左半分になる

Exercise33.

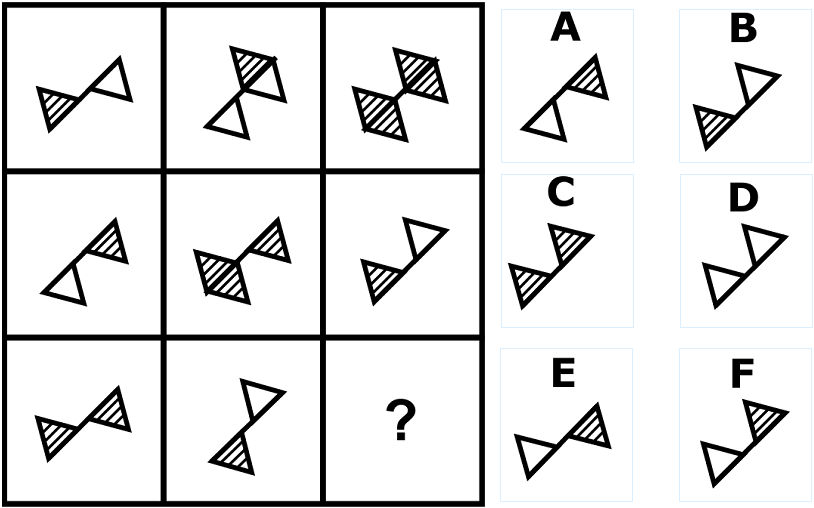
問33の答え「E」

新 :: 問33の解説 2022.12.26 追記

• 右上り斜めでグルーピングする
• 上段から中段へ ：右上の三角形がある場合は、反対側に反転。
  上段から中段へ：右上の三角形がない場合は、右下の三角形が反対側に反転。
• 中段から下段へ：左下の三角形がある場合は、反対側に反転。
  中段から下段へ：左下の三角形がない場合は、左上の三角形が反対側に反転。

問33の解説

• 斜めでグルーピングする
• それぞれの旗を反対方向に上下どちらかで1回だけ折り返すと、左下の画像になる。

問33の解説2

• 上側の旗を上側の別の旗に向けて折り返すと、中段１個左側の図形となる。
• 中段の旗を下側の別の旗に向けて折り返すと、下段１個左側の図形となる。

問33の詳しい解説

• 問題のそれぞれのマスに記号を振る。
  a | b | c
  d | e | f
  g | h | i
• 斜めでグルーピングすると、3つのグループができる。
  c – e – g
  b – d – i
  a – f – h
• 問題のそれぞれ”旗のような記号”に番号を振る。
  1 / 2
  3 / 4
  
• 上段右側( c )：1番の旗を2番の旗に向けて折り返すと、中段真中の画像( e )となる。
• 中段真中( e )：3番の旗を4番の旗に向けて折り返すと、下段左側の画像( g )となる。
• 上段真中( b )：1番の旗を2番の旗に向けて折り返すと、中段左側の画像( d )となる。
• 中段左側( d )：4番の旗を3番の旗に向けて折り返すと、下段右側の画像( i )となる。
• 上段左側( a )：2番の旗を1番の旗に向けて折り返すと、中段右側の画像( f )となる。
• 中段右側( f )：3番の旗を4番の旗に向けて折り返すと、下段真中の画像( h )となる。

*:この問題を難しくしている原因は2つある。ひとつは、従来ならば問題を解く時に横でグルーピングをする所を、斜めでグルーピングする点。ふたつめは、それぞれのグループで別の規則性に従って変化する点。緑色では1番が2番に、3番が4番に移動しているが、赤色では1番が2番に、4番が3番に移動し、青色では、2番が1番に、3番が4番に移動している。
　この問題の法則性に納得できないのなら、IQ140は越えれないし、IQ140もないのにこの問題と製作者に文句を言うのなら、自分の知性には柔軟性がないと口外しているようなものだ。問題製作者にはこちら側には見えていない世界が見えているのかもしれないのだから。
　この問題が、横割りで、旗の変化の法則性により統一感があったのなら、IQ140を隔てる問題とはならなかったはずだ。「もう少し問題の難易度を下げてよ」と言うのはお門違いだし、”問題の美しさ” を問うてもそれも別の問題だ。
　しかし、それでもなお、この問題の解説は辻褄が合うだけで、一言で美しく解説しているとは言い切れない。この問題にはまだ見えていない法則性が隠れているのだろうか。

Exercise34.

問34の答え「A」

問34の解説

• 黒丸を障害物のように見る。
• 「◯◯」が縦棒の周りを一周するように動く。
• 「◯」が「●」の上にきたら塗り潰されて「●」になる。

Exercise35.

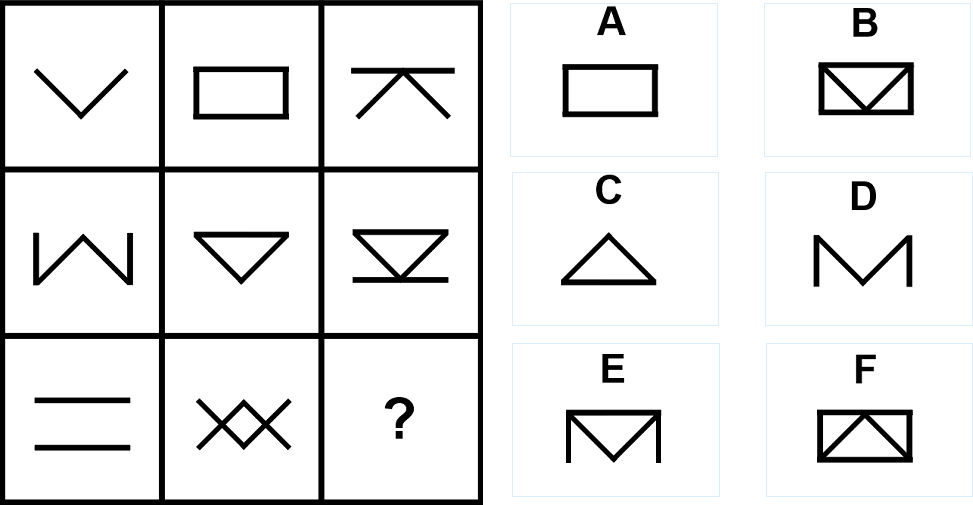
問35の答え「D」

問35の解説

各記号は次の五種類の要素に分解できる。

仮称	上下	左右	山	谷	上
要素	＝	| |	∧	V	ー

各要素は2組みの配列に分類できる。

組	1番目	2番目	3番目
第一組	V	＝	∧
第二組	V	| |	ー

上記の表を頼りに好きな所から要素を埋めていく。ただし、左側上段では「V」が、左側下段では「＝」と「ー」が重なっている点に注意が必要。重なっていて1つの記号に見える場所には赤と青で色を付けた。

段	左側で使う記号	真ん中で使う記号	右側で使う記号
上段：第一組	V	＝	∧
上段：第二組	V	| |	ー
中段：第一組	∧	V	＝
中段：第二組	| |	ー	V
下段：第一組	＝	∧	? = V
下段：第二組	ー	V	? = | |

よって、答えは「 D 」となる。

全問正解 Result of IQ Test :: IQ145 or more

まとめ

ヤフー知恵袋

パソコンのパスワードを見つける方法に総当たり攻撃がある。同様に、IQテストの答えも総当たりで試行するといずれは全問正解に行き着く。しかしそれでは、何故その答えになったのか、肝心の答えを導いた法則性がわからない。結局、答えと選択肢と問題を見比べ、辻褄合わせの法則性をでっち上げることになるが、正しい経路で導き出された答えではないので、でっち上げの法則性ではどこかで矛盾が生じる。

今回、Exercise33はヤフー知恵袋を参考にさせてもらった。

Exercise34はこちらの動画を参考にさせていただきました。

最後までご覧いただき、ありがとうございました。参考になれば幸いです。🙇‍♂️