こんにちは。宮野川です。個人でIQテスト作ってます。以前遊んだハイレンジIQテストの結果はIQ151(s.d.15) です。
この記事では、2021年IQテスト(2021年度 新証明書)答えを全18問図解で解説しています。
また、答えの一覧を一枚の画像にまとめました。手取り早く答えだけを知りたい方は、そちらをご覧ください。
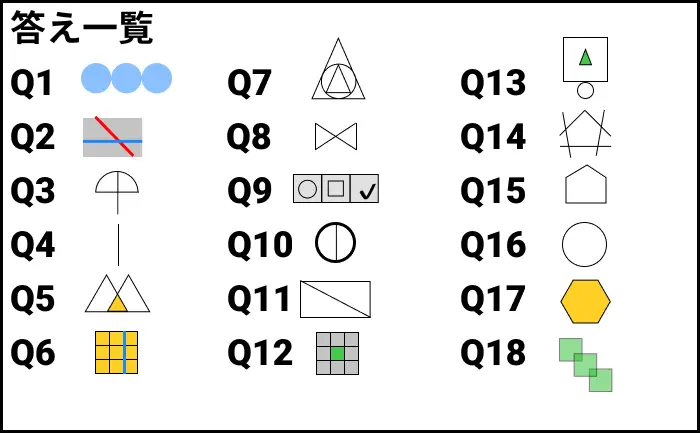
答えの一覧を一枚の画像で見る
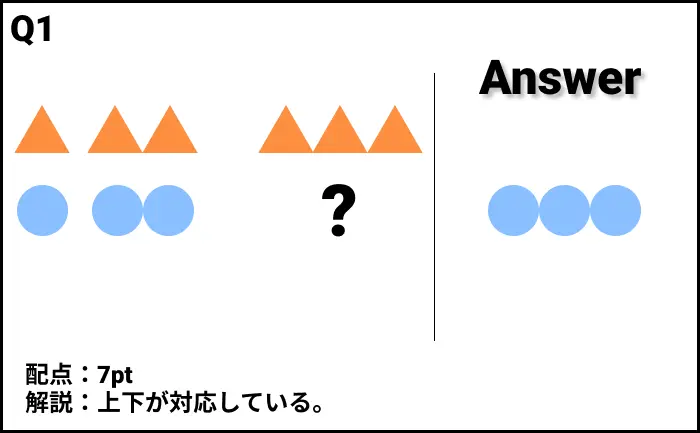
Q1の答え
解説
- 上下が対応している。
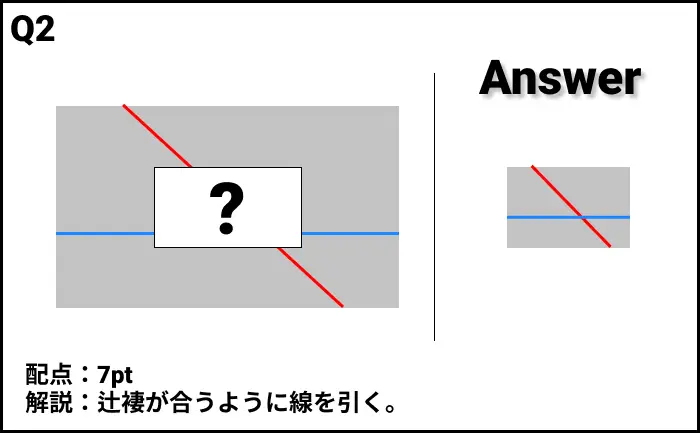
Q2の答え
解説
- 辻褄が合うように線を引く。
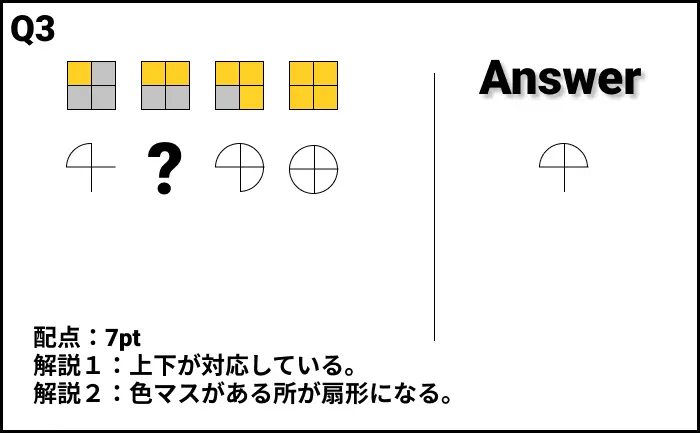
Q3の答え
解説
- 解説1:上下が対応している。
- 解説2:色マスのある所が扇形になる。
Q4の答え
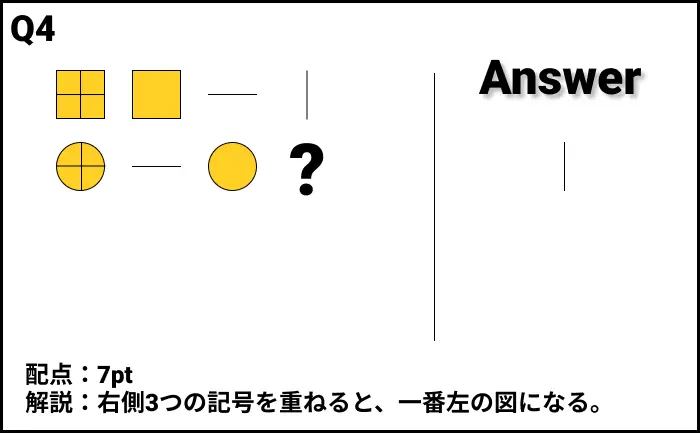
解説
- 解説:右側3つの記号を重ねると、一番左の図になる。
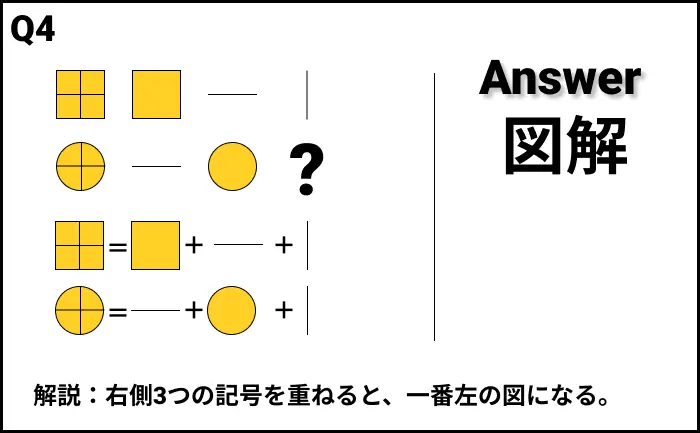
Q5の答え
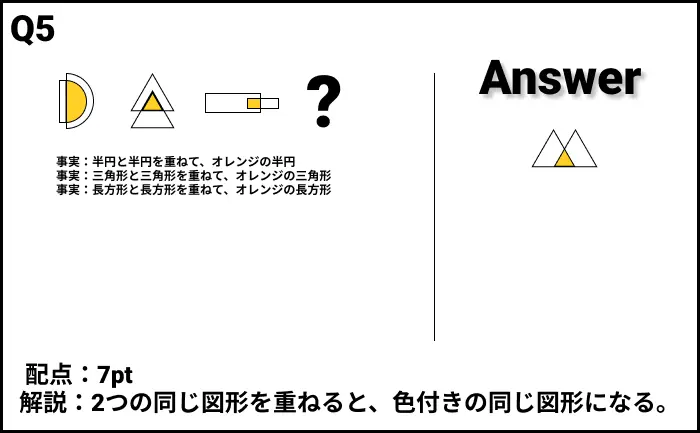
解説
- 解説:2つの同じ図形を重ねると、色付きの同じ図形になる。
Q6の答え
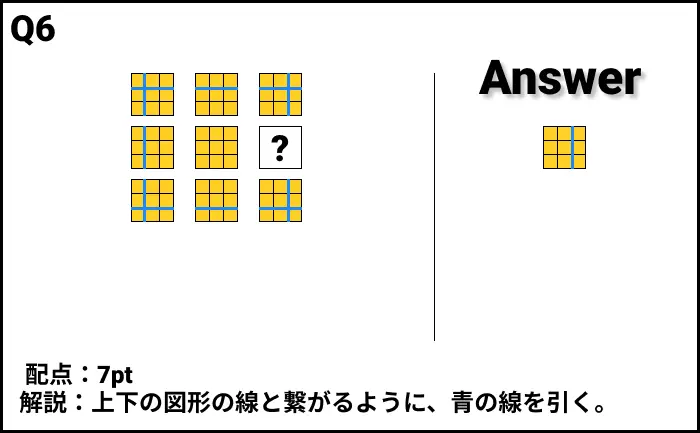
解説
- 解説:上下の図形の線と繋がるように、青の線を引く。
Q7の答え

解説
- 解説:左の図に、真ん中の図を入れると、右の図になる。
Q8の答え
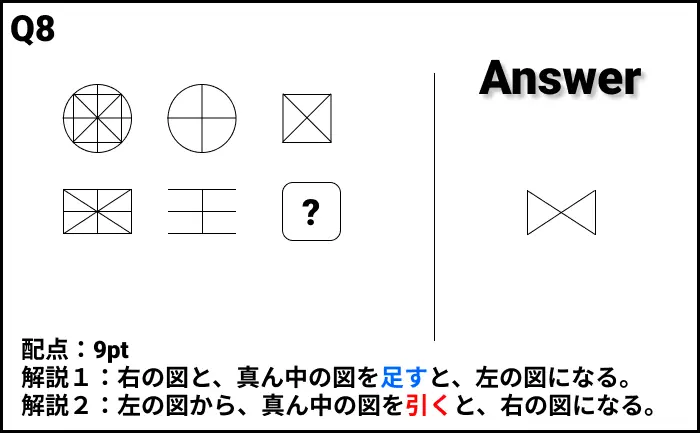
解説
- 解説1:右の図と、真ん中の図を足すと、左の図になる。
- 解説2:左の図から、真ん中の図を引くと、右の図になる。
Q9の答え
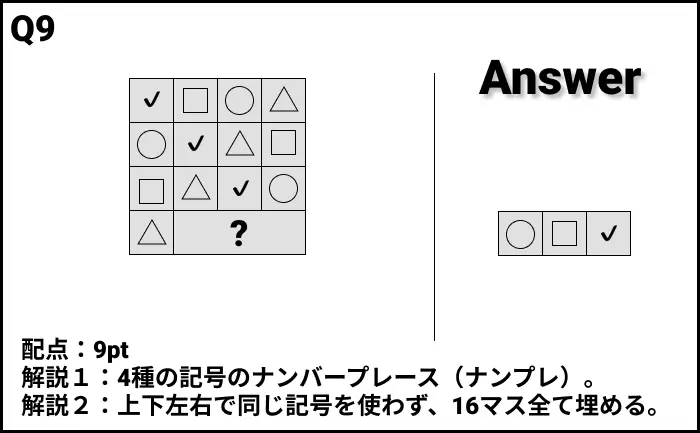
解説
- 解説1:4種の記号のナンバープレース(ナンプレ)。
- 解説2:上下左右で同じ記号を使わず、16マス全て埋める。
- 解説3:縦割り、横割り、重複なしで「✔️」「□」「◯」「△」を使う。
Q10の答え
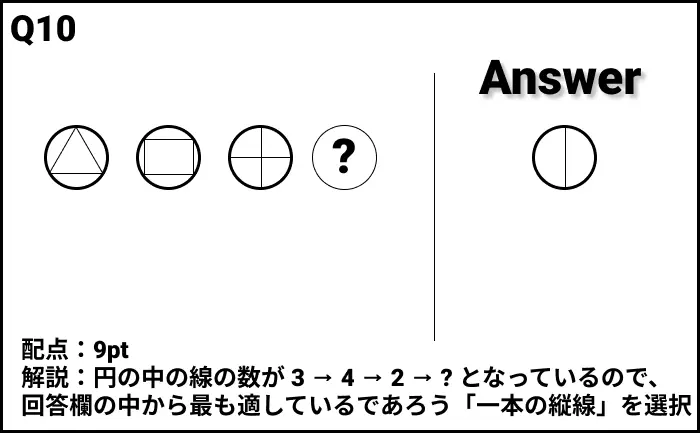
解説
- 解説:円の中の線の数が 3 → 4 → 2 → ? となっている。回答欄の中から最も適しているであろう「一本の縦線」を選択
Q11の答え
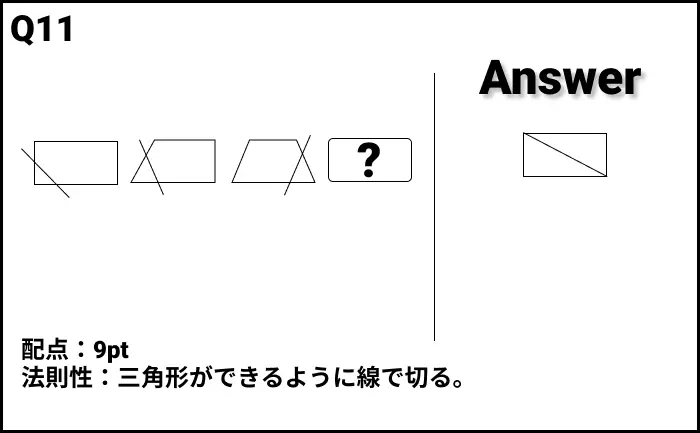
解説
- 法則性:三角形ができるように線で切る。
Q12の答え
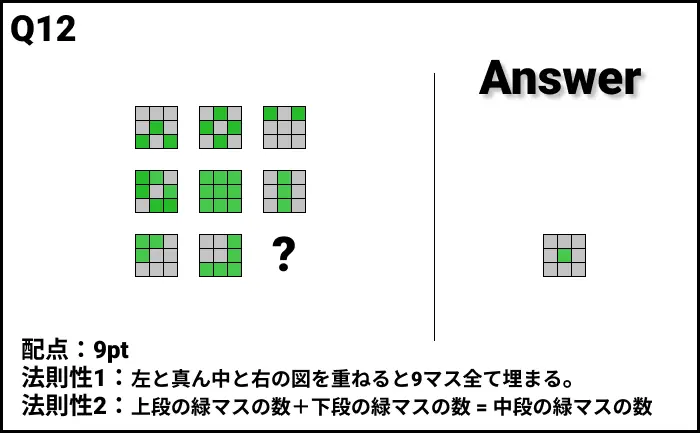
解説
- 法則性:左と真ん中と右の図を重ねると9マス全て埋まる。
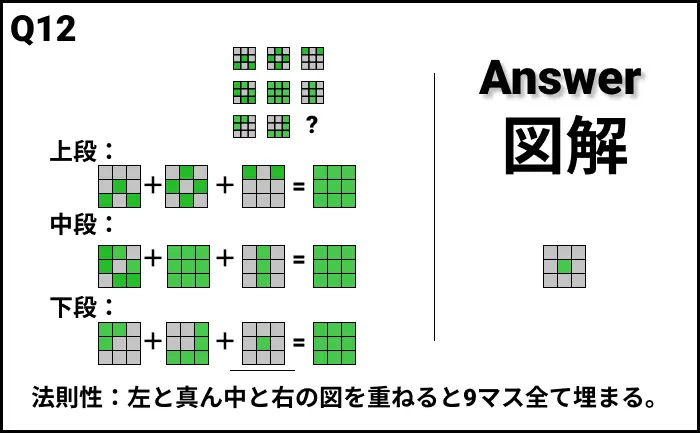
解説2
- 法則性2:上段の緑マスの数 + 下段の緑マスの数 = 中段の緑マスの数

情報提供
コメント欄『にぇ』さんより。情報感謝します。
Q13の答え
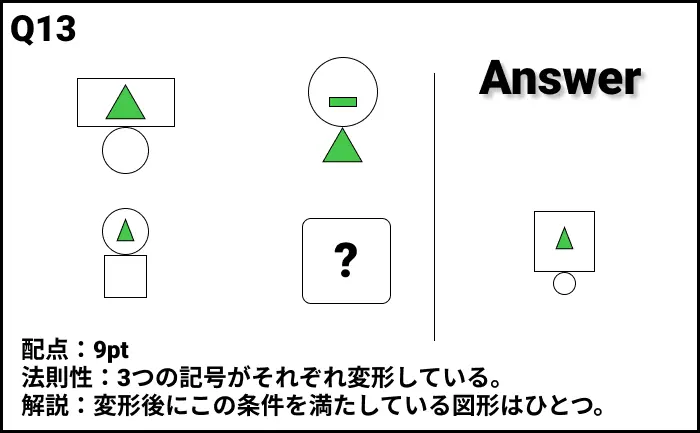
解説
- 法則性:3つの記号がそれぞれ変形している。
- 解説:変形後にこの条件を満たしている図形はひとつ。
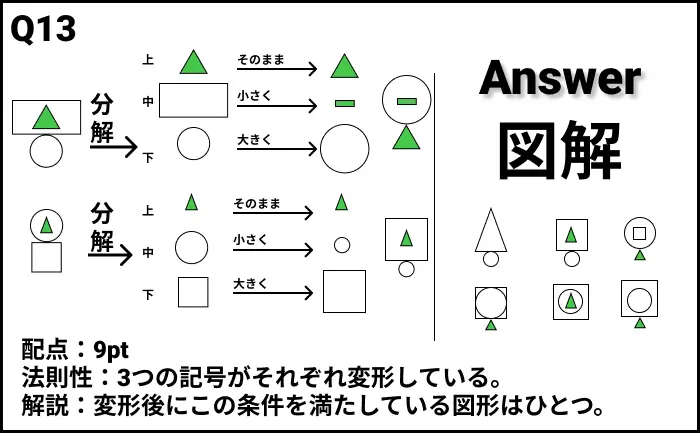
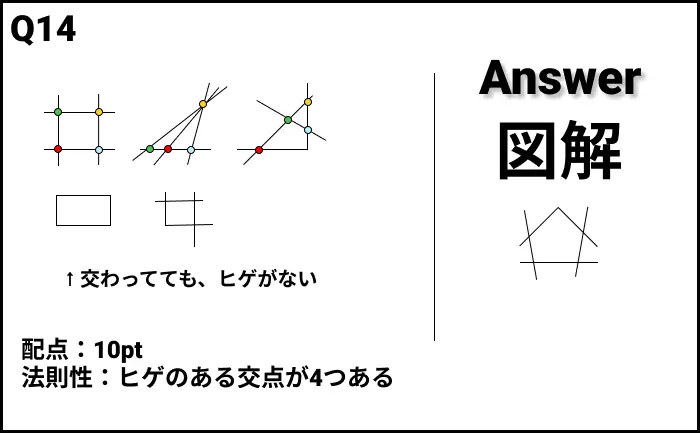
Q14の答え
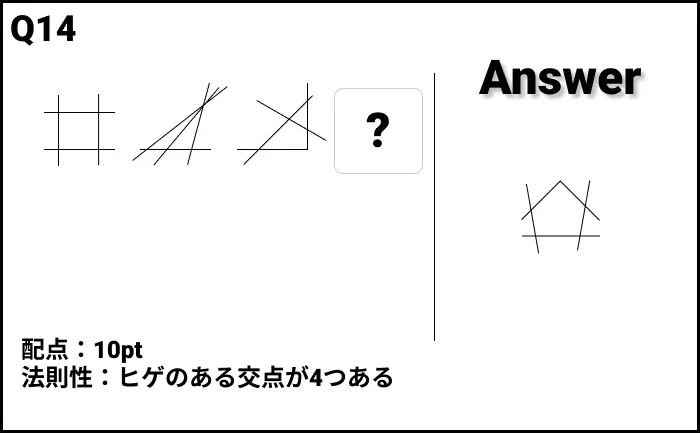
解説
- 法則性:ヒゲのある交点が4つある
- 線が交わっていても、線が飛び出ていない、繋がっている場合は数えない。
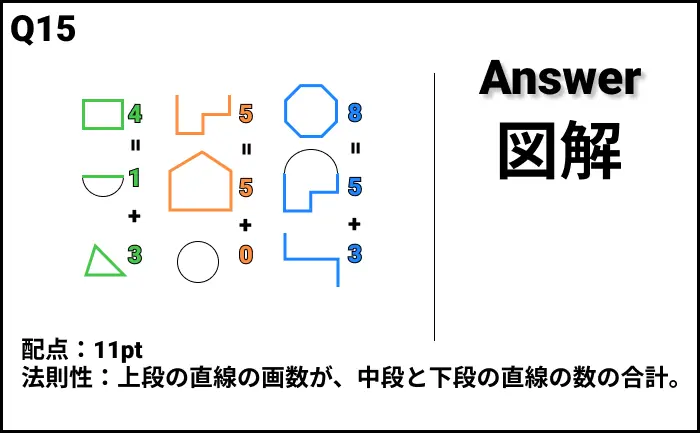
Q15の答え
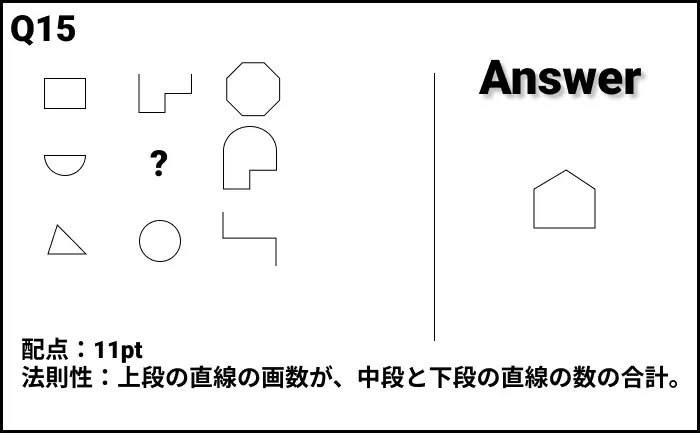
解説
- 法則性:上段の直線の画数が、中段と下段の直線の数の合計。
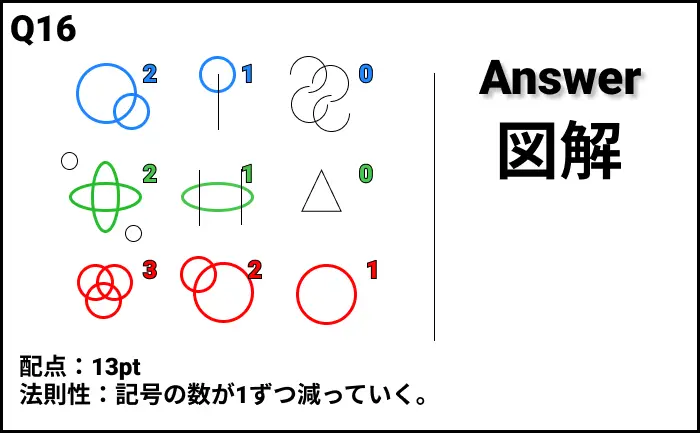
Q16の答え
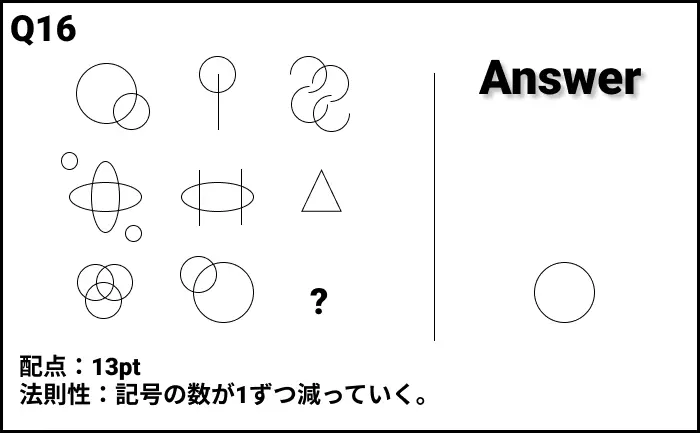
解説
- 法則性:記号の数が1ずつ減っていく。
- 上段:円の数が2→1→0
- 中段:楕円の数が2→1→0
- 下段:縁の数が3→2→1
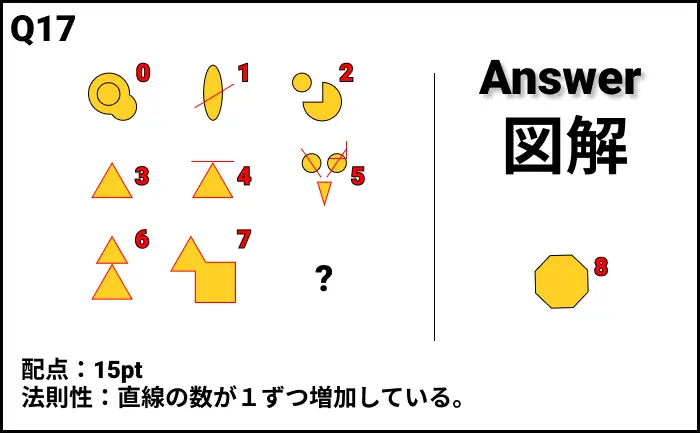
Q17の答え
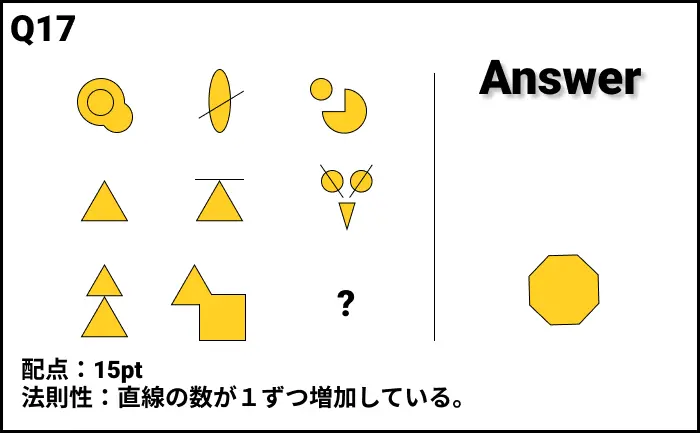
解説
- 法則性:直線の数が1ずつ増加している。
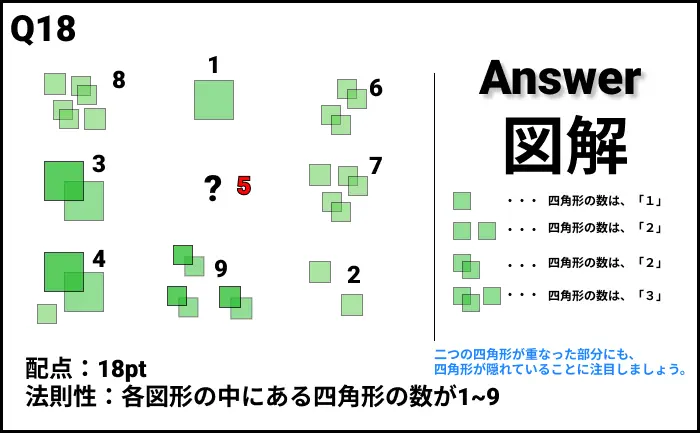
Q18の答え

解説
- 法則性:各図形の中にある四角形の数が1〜9。
- 二つの四角形が重なった部分にも、四角形が隠れていることに注意しましょう。
コメント欄の「み」さんのコメントより。感謝します。
18/18の正解で…
A Real Me の今までのIQテストの答えと解説一覧はこちら
参照元
2021年IQテスト(2021年度 新証明書)[ https://www.arealme.com/iq-2021/ja/ ]

Q14は、交点の数が4個だからだと思います。
Unknown さん
コメントありがとうございます。
交点が4つは良い着眼点と思います。

しかし、交点が4つの選択肢は他にもあります。
そうでしたか…!
ろくに確認もせずにすみません
こんにちは!
18の問題は、各図形の四角形を数えると、1.2.3.4.6.7.8.9となっているので、?の所が5つ四角形があるものが答えになると思いました!
みさん、こんにちは
情報ありがとうございます。おかげさまで謎が解けました。
ブログ記事に反映させていただきます。
法則性がわかると、算数の問題であった、ピラミッドの中の三角形の数を求めよと似てますね。
情報提供感謝します。
質問失礼します。
Q17は六角形がなぜ直線が8本になるのでしょうか。
こ さん
コメント有難うございます。
画像作成ミスです。
Q17の画像を正答の八角形に修正いたしました。
訂正してお詫び申し上げます。
Q10は、選択肢に1本の線の図形が他にもありますので…
「円の中心として回転対称の図形を選ぶ問題」
って解釈のほうがしっくり来る気がしますね。
Q12は、他の選択肢にも9マス全て埋まる図形があるのでしっくり来ませんね…
「上の緑の数+下の緑の数=中の緑の数(3+3=6、4+5=9、2+1=3)」はどうでしょうか。
Q13は、なぜ長方形が緑になるのか説明されないのがしっくり来ませんね…
「下の図形の中に上の図形を入れたとき、一番角の少ない図形を下に出し、中に残った図形は緑に塗る」
とかいう複雑怪奇な(個人的に美しくもない)法則になりそうですね…
もっと良い解釈がありそうな…
Q14は、線を伸ばして交差してできる図形の個数が増えるような順とかでしょうか…
1つ目は四角形が1つ
2つ目は三角形が2つ
3つ目は四角形が1つ、三角形が2つで合計3つ
4つ目は五角形が1つ、三角形が5つで合計6つ
(あまりしっくり来てませんが…)
Q15以降は面白い法則性があるもんだなと関心しました
勉強になりました
にぇ さん
コメントありがとうございます。
仮想通貨に夢中になっててブログのこと放置しておりました。
コメントを参考に解説と図解を改めさせていただきます。
情報感謝します。