ノルウェーメンサの答え Exercise 1〜35
この記事には『ノルウェーメンサの答え』が書かれています。
全35問の答えと解説、さらには図解も付いています。
久しぶりにGoogle Analytics の解析画面を見ました。『ノルウェーメンサの答え』で検索してこのブログに来られた方がいました。さっそく『ノルウェーメンサ』をやってみました。
- IQ Test Made by Mensa Norway
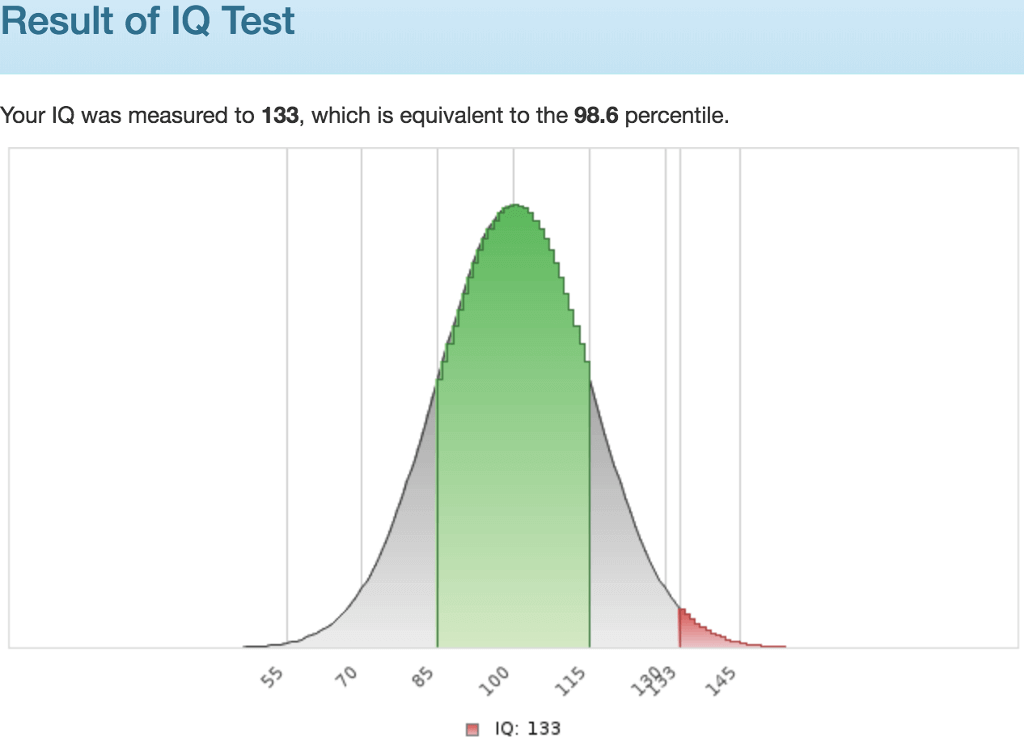
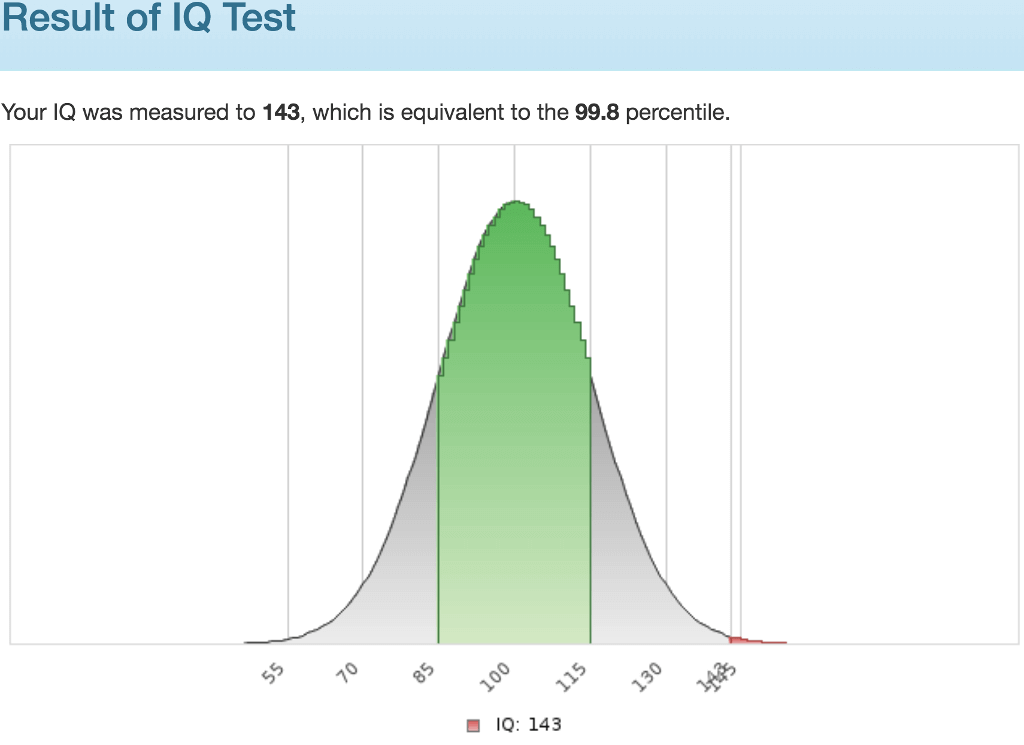
私の初回スコアは133, パーセンタイルは98.6%でした。2回目に遊んだ時は143, パーセンタイル99.8%でした。

ノルウェーメンサの答え
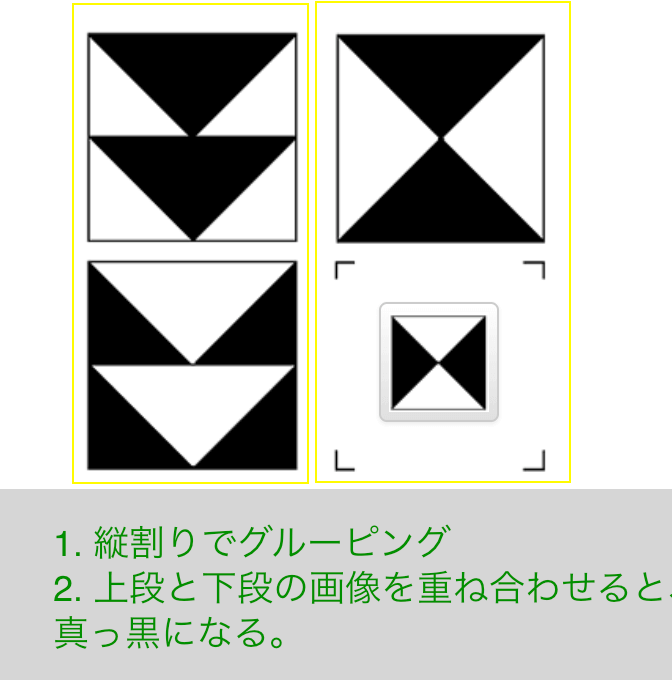
Exercise 1
解説
- 縦割りでグルーピング
- 上段と下段の画像を重ね合わせると、真っ黒になる。
Exercise 2

解説
- 縦割りでグルーピング
- 上下の画像を重ね合わせると、真っ黒になる
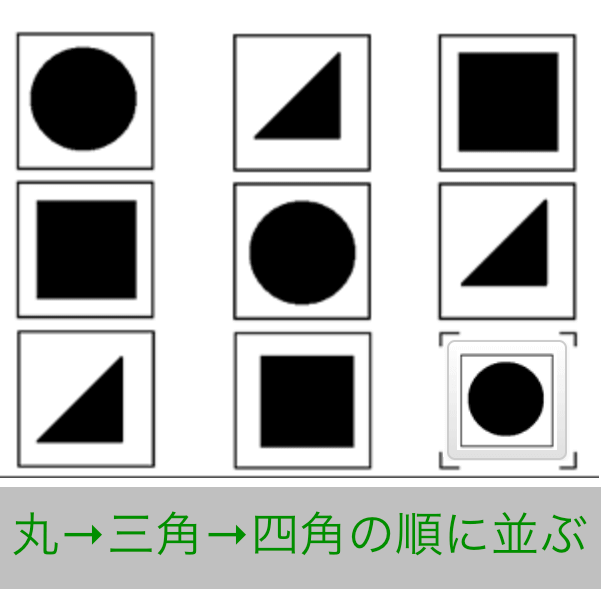
Exercise 3
解説
- 丸→三角→四角 の順で並ぶ
Exercise 4
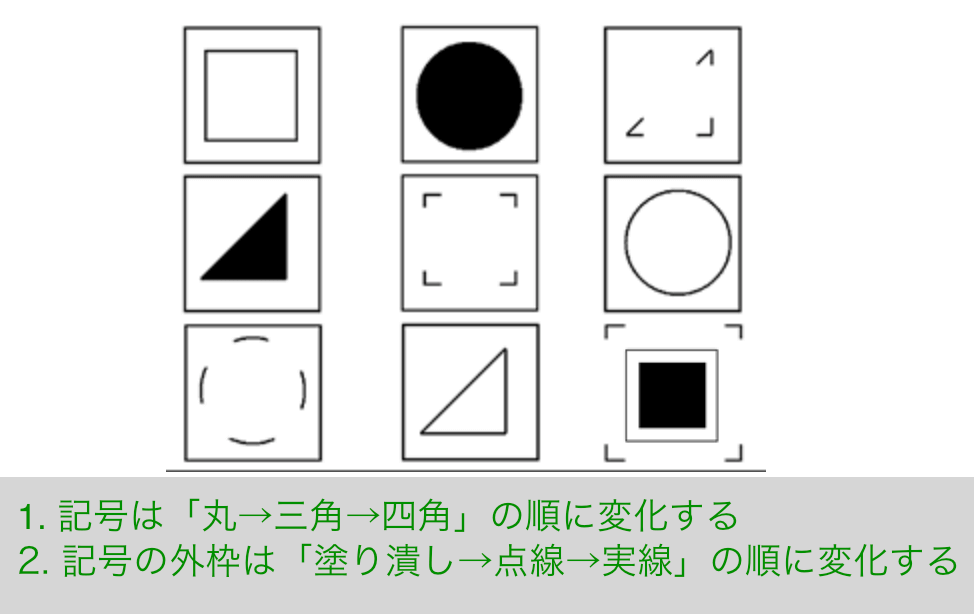
解説
- 記号は「丸→三角→四角」の順に変化する
- 記号の外枠は「塗り潰し→点線→実線」の順に変化する
Exercise 5
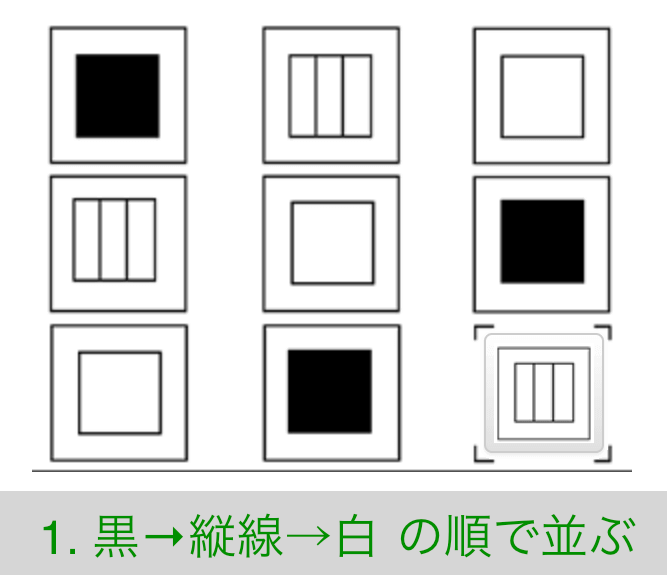
解説
- 黒→縦線→白 の順で並ぶ
Exercise 6
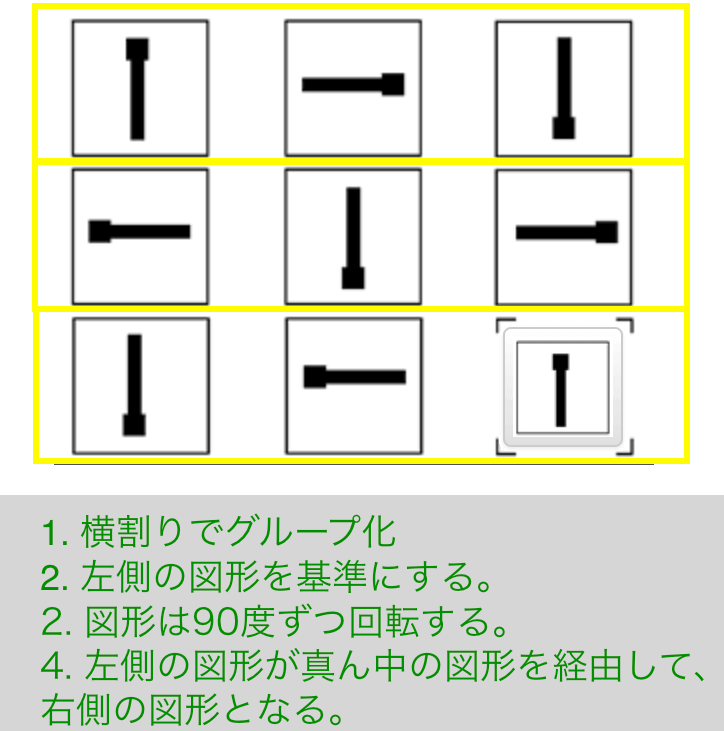
解説
- 横割りでグルーピング
- 左側の図形を基準にする。
- 図形は90度ずつ回転する。
- 左側の図形が真ん中の図形を経由して、右側の図形となる。
Exercise 7
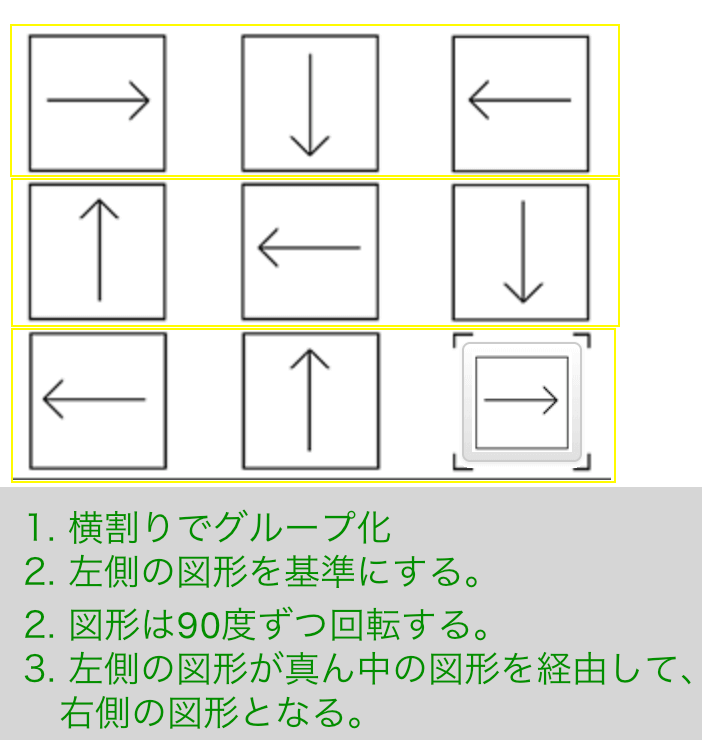
解説
- 横割りでグルーピング
- 左側の図形を基準にする。
- 図形は90度ずつ回転する。
- 左側の図形が真ん中の図形を経由して、右側の図形となる。
Exercise 8
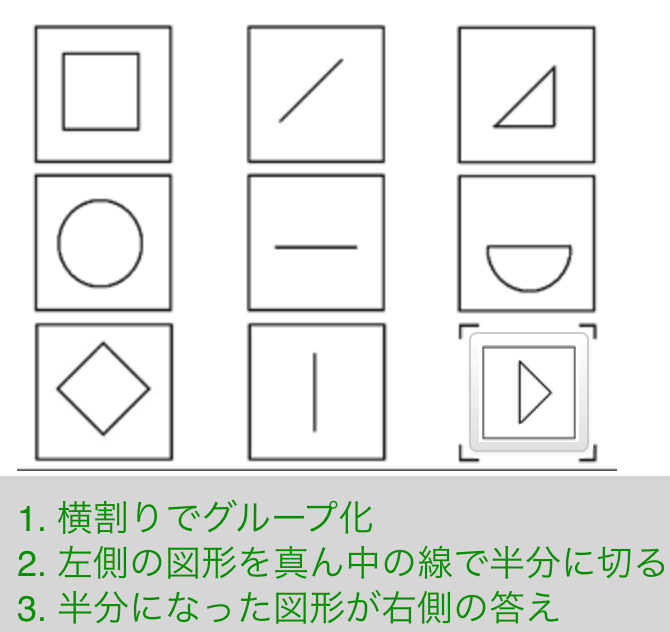
解説
- 横割りでグルーピング
- 左側の図形を真ん中の線で半分に切る
- 半分になった(右下を含む)図形が右側の答え
Exercise 9
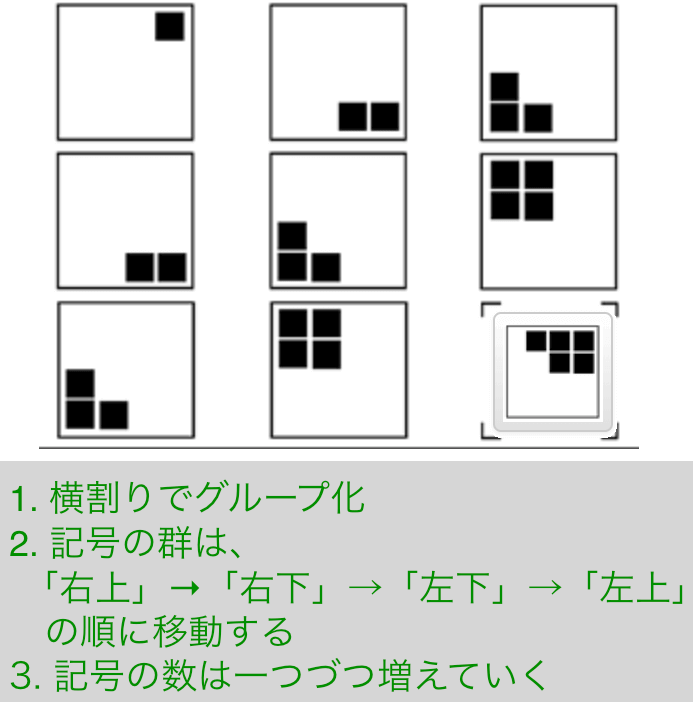
解説
- 横割りでグルーピング
- 記号の群は、「右上」→「右下」→「左下」→「左上」の順に移動する
- 記号の数は一つづつ増えていく
Exercise 10
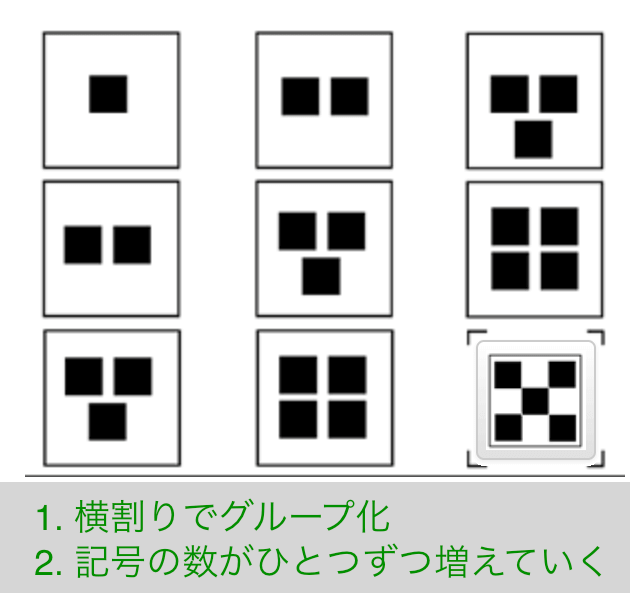
解説
- 横割りでグルーピング
- 記号の数がひとつずつ増えていく
Exercise 11
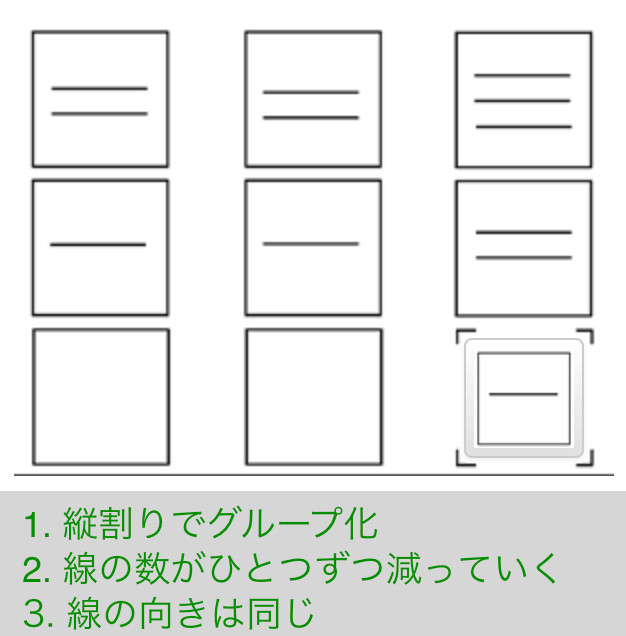
解説
- 縦割りでグルーピング
- 線の数がひとつずつ減っていく
- 線の向きは共通して同じ
Exercise 12
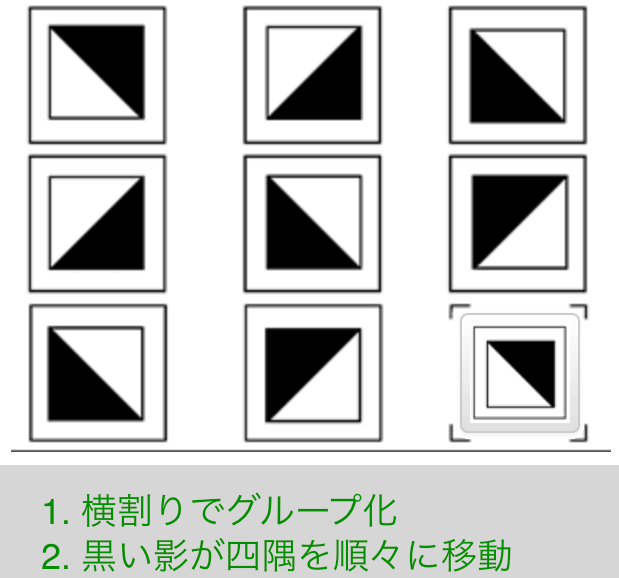
解説
- 横割りでグルーピング
- 黒い影が四隅を順々に移動(「右上」→「右下」→「左下」→「左上」)
Exercise 13
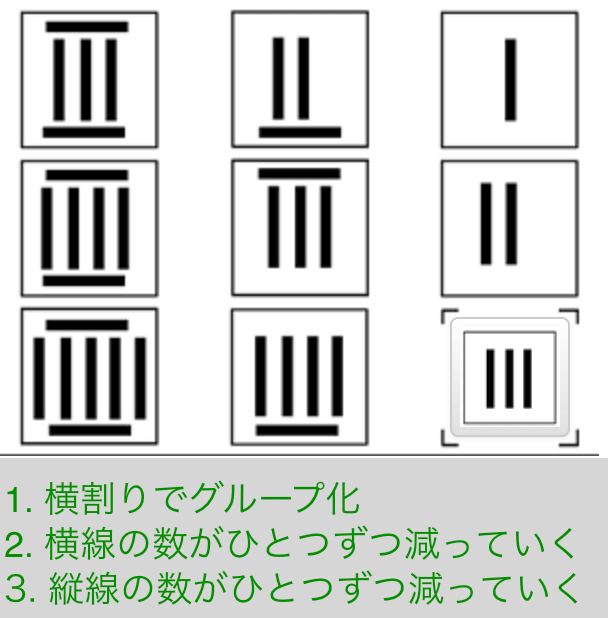
解説
- 横割りでグルーピング
- 横線の数がひとつずつ減っていく
- 縦線の数がひとつずつ減っていく
Exercise 14
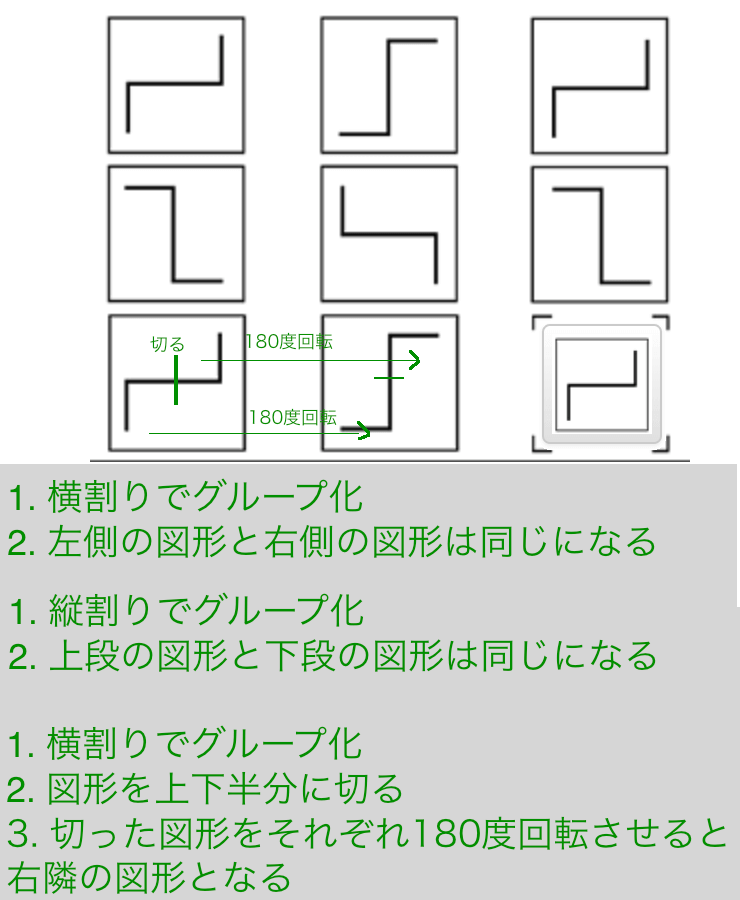
解説その1
- 横割りでグルーピング
- 左側の図形と右側の図形は同じになる
解説その2
- 縦割りでグルーピング
- 上段の図形と下段の図形は同じになる
解説その3
- 横割りでグルーピング
- 図形を上下半分に切る
- 切った図形をそれぞれ180度回転させると右隣の図形となる
Exercise 15
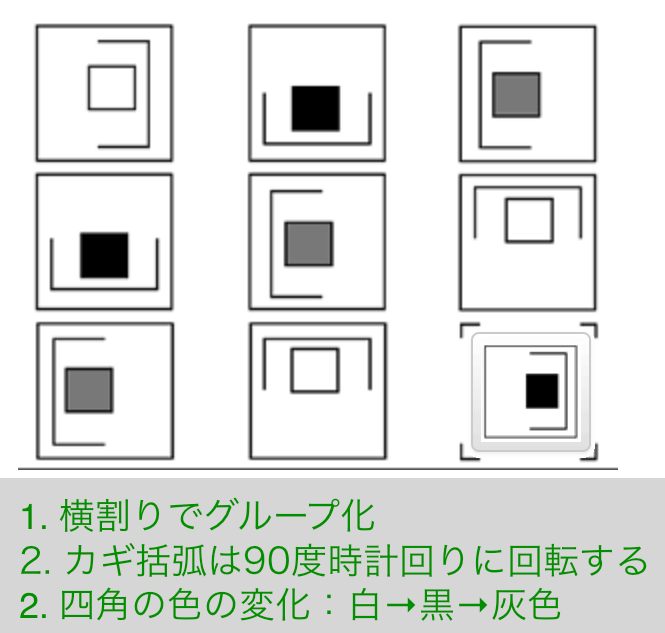
解説
- 横割りでグルーピング
- カギ括弧は90度時計回りに回転する
- 四角の色の変化:白→黒→灰色
Exercise 16
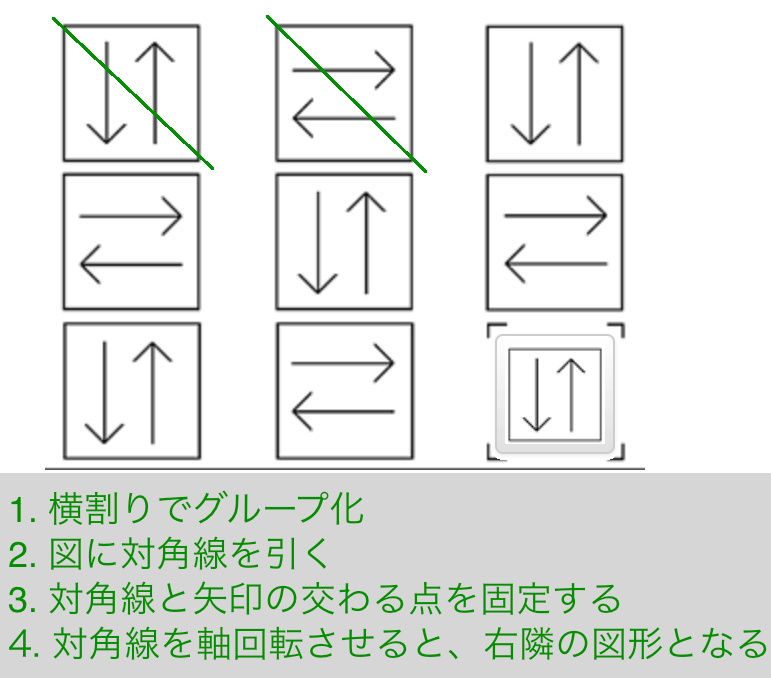
解説その1
- 横割りでグルーピング
- 図に対角線を引く
- 対角線と矢印の交わる点をそれぞれ固定する
- 対角線を軸回転させると、右隣の図形となる
解説その2
- 横割りでグルーピング
- 左側の図形と右側の図形は同じになる
解説その3
- 縦割りでグルーピング
- 上段の図形と下段の図形は同じになる
Exercise 17
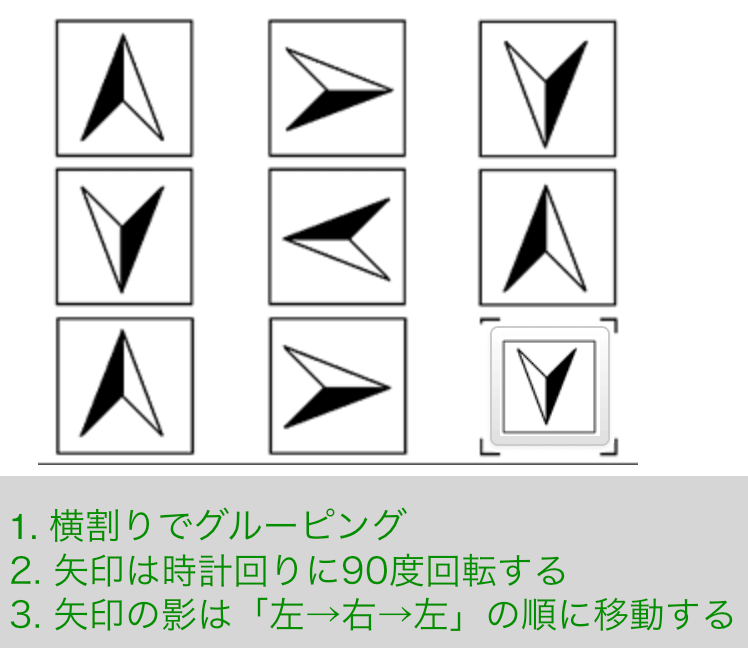
解説
- 横割りでグルーピング
- 矢印は時計回りに90度回転する
- 矢印の影は「左→右→左」の順に移動する
Exercise 18

解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせると、右側の図形になる。
- 黒色と黒色が重なり合った場合、その場所は白色になる。
- 白+白=白
- 黒+白=黒
- 黒+黒=白
解説2
- 縦割りでグルーピング
- 上段の図形と中段の図形を重ね合わせると、下段の図形になる。
- 左側外 白+黒=黒 … A
- 左側内 黒+黒=白 … B
- 真中外 黒+黒=白 … B
- 真中内 白+白=白 … C
- 右側外 黒+白=黒 … A
- 右側内 黒+黒=白 … B
Exercise 19
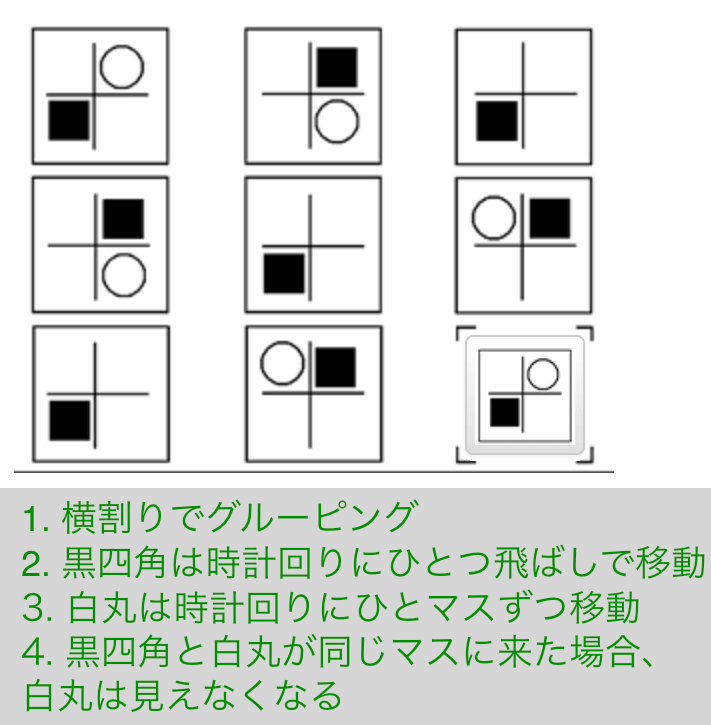
解説
- 横割りでグルーピング
- 黒四角は時計回りにひとつ飛ばしで移動
- 白丸は時計回りにひとマスずつ移動
- 黒四角と白丸が同じマスに来た場合、白丸は見えなくなる
Exercise 20
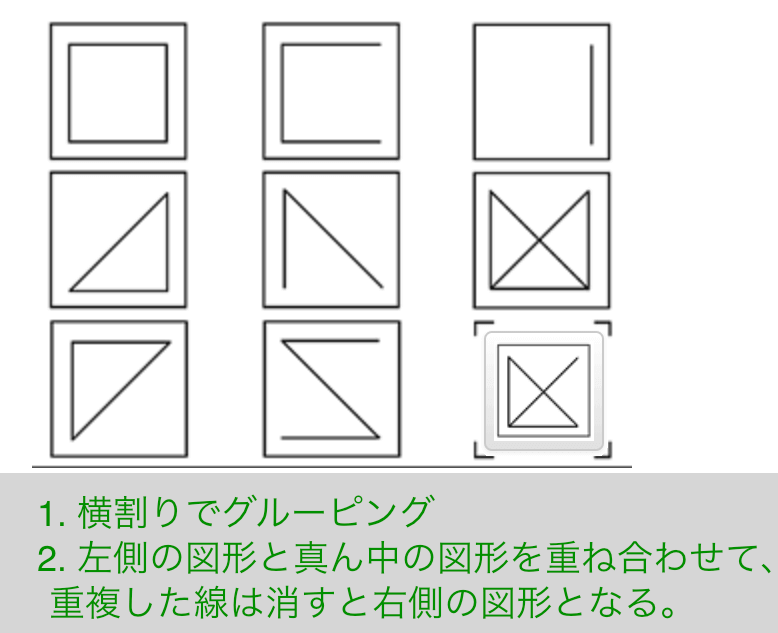
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、重複した線は消すと右側の図形となる。
Exercise 21
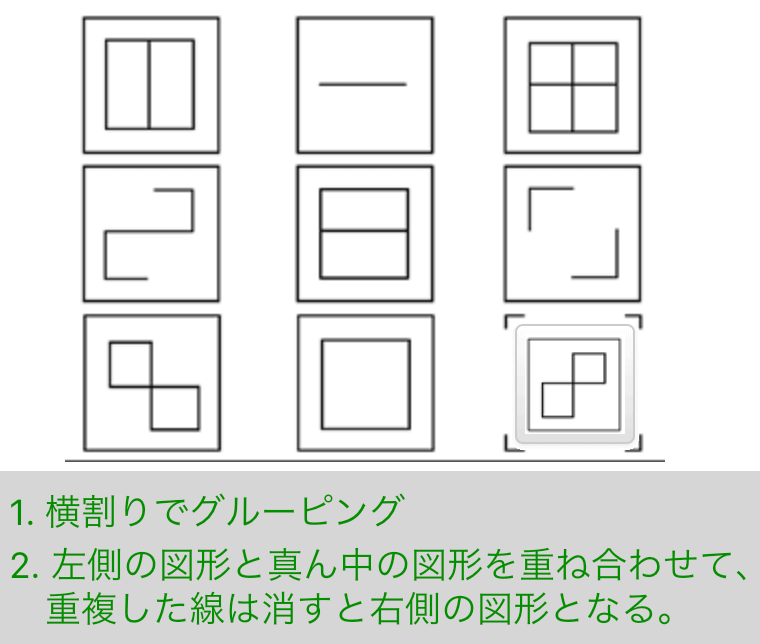
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、重複した線は消すと右側の図形となる。
Exercise 22
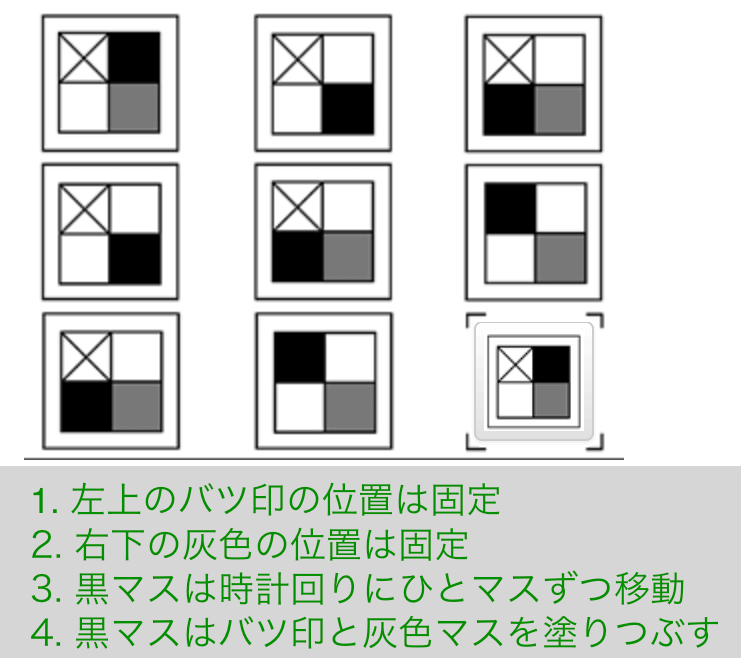
解説
- 左上のバツ印の位置は固定
- 右下の灰色の位置は固定
- 黒マスは時計回りにひとマスずつ移動
- 黒マスはバツ印と灰色マスを塗り潰す
Exercise 23
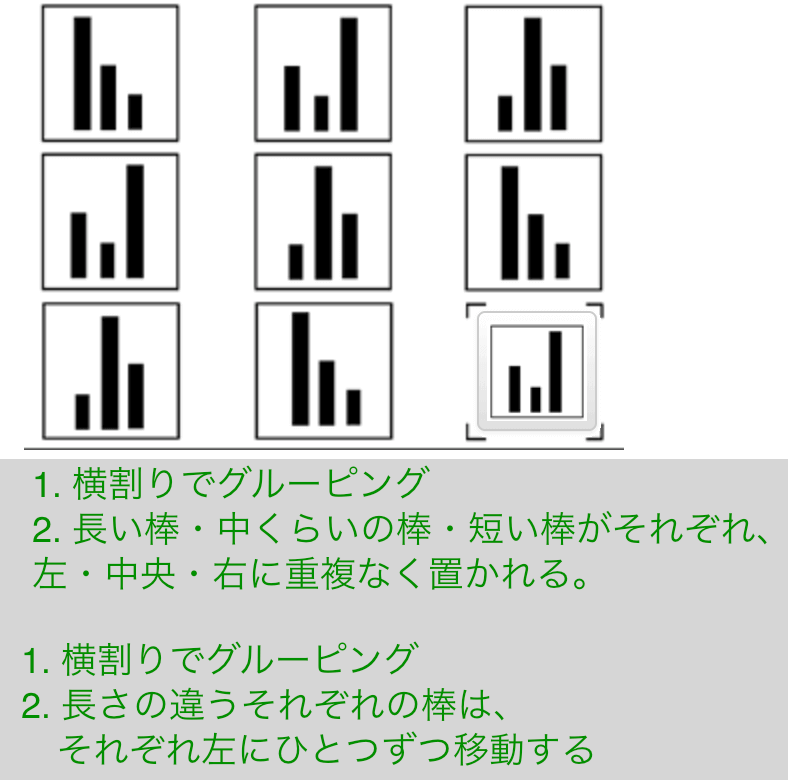
解説その1
- 横割りか縦割りでグルーピング
- 長い棒・中くらいの棒・短い棒がそれぞれ、左・中央・右に重複なく置かれる。
解説その2
- 横割りでグルーピング
- 長さの違うそれぞれの棒は、 それぞれ左にひとつずつ移動する。
Exercise 24
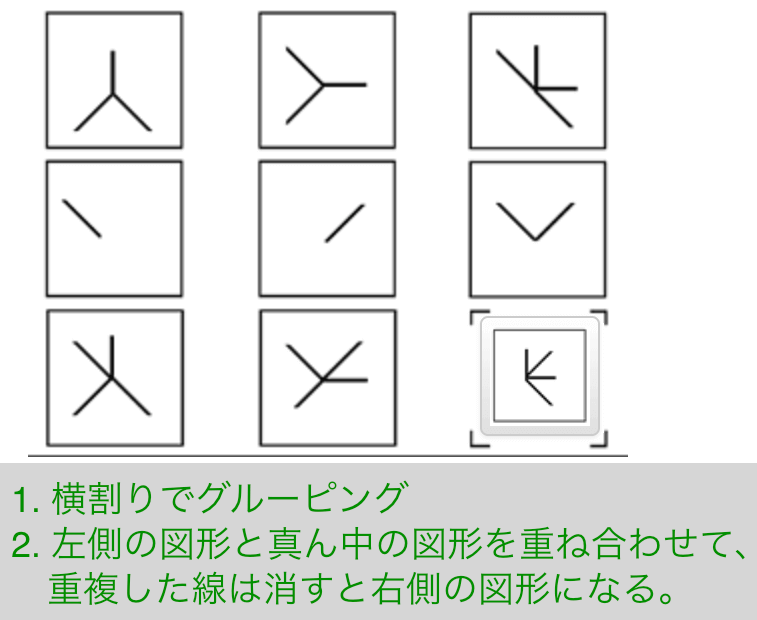
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、 重複した線を消すと右側の図形になる。
Exercise 25
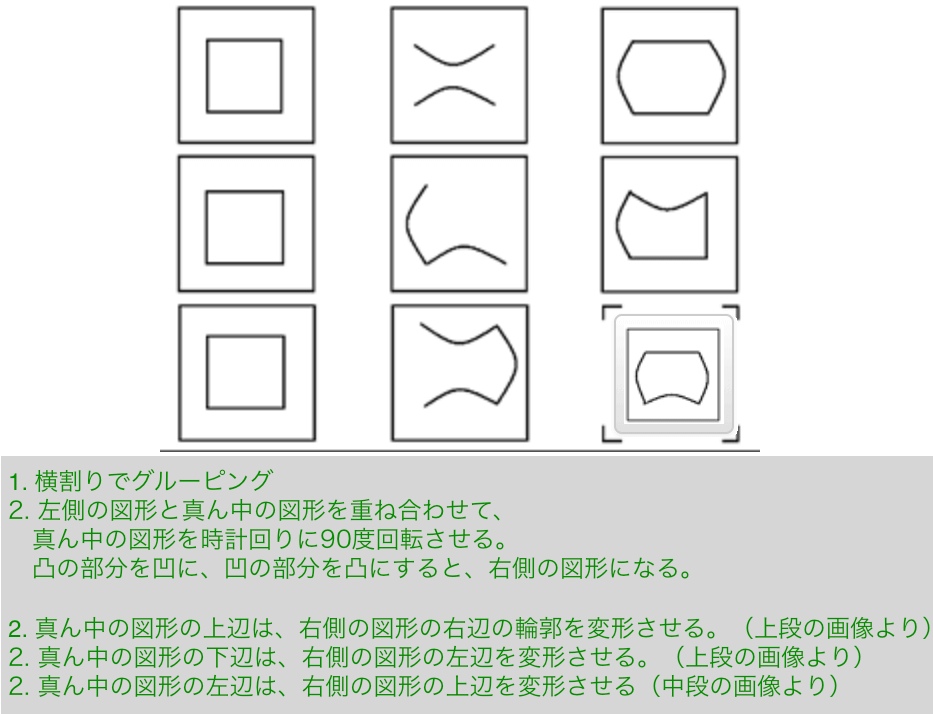
解説その1
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、真ん中の図形を時計回りに90度回転させる。
- 真ん中の図形の凸の部分を凹に、凹の部分を凸にすると、右側の図形になる。
解説その2
- 真ん中の図形の上辺は、右側の図形の右辺の輪郭を変形させる。(上段の画像より)
- 真ん中の図形の下辺は、右側の図形の左辺の輪郭を変形させる。(上段の画像より)
- 真ん中の図形の左辺は、右側の図形の上辺の輪郭を変形させる。(中段の画像より)
- 真ん中の図形の右辺は、右側の図形の下辺の輪郭を変形させる。(1. 2. 3. より)
Exercise 26
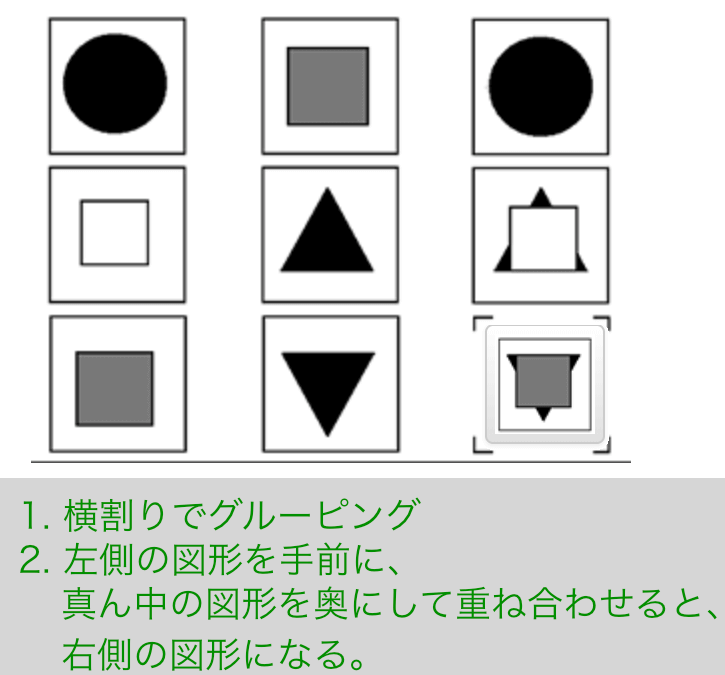
解説
- 横割りでグルーピング
- 左側の図形を手前に、真ん中の図形を奥にして重ね合わせると、右側の図形になる。
Exercise 27
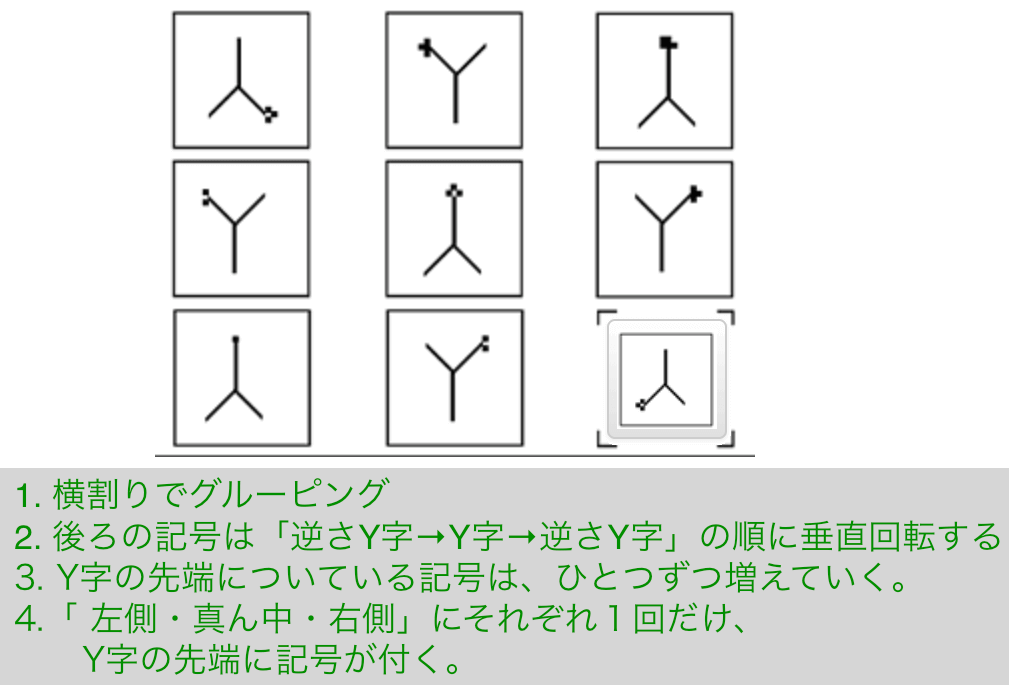
解説
- 横割りでグルーピング
- 後ろの記号は「逆さY字→Y字→逆さY字」の順に垂直回転する
- Y字の先端についている記号は、ひとつずつ増えていく。
- 「 左側・真ん中・右側」にそれぞれ1回だけ、Y字の先端に記号が付く。
Exercise 28
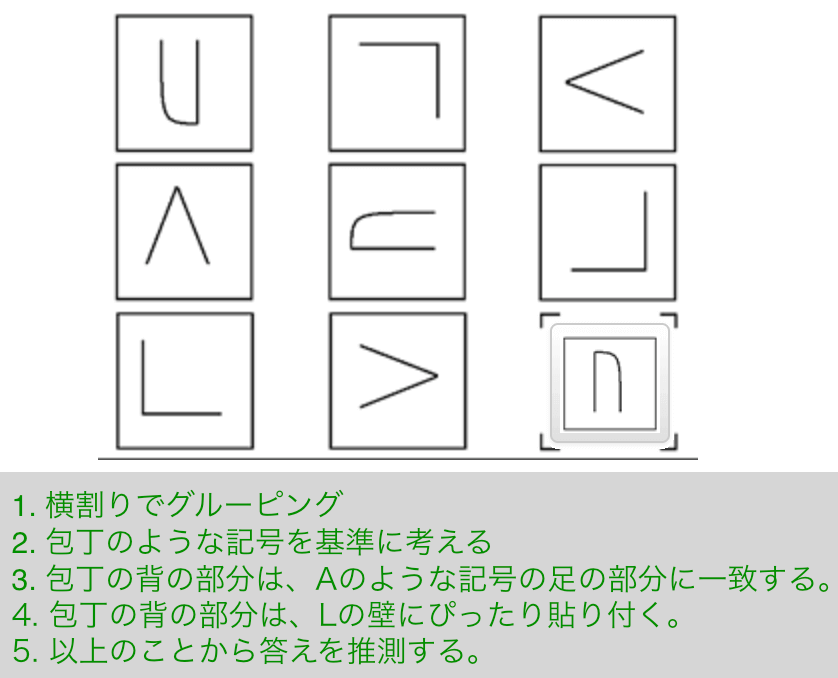
解説
- 横割りでグルーピング
- 包丁のような記号を基準に考える
- 包丁の背の部分は、Aのような記号の足の部分に一致する。
- 包丁の背の部分は、Lの壁にぴったり貼り付く。
- 以上のことから答えを推測する。
解説2
- 横割りでグルーピング
- 記号は右下に降りるごとに、時計回りに90度ずつ回転する。
Exercise 29
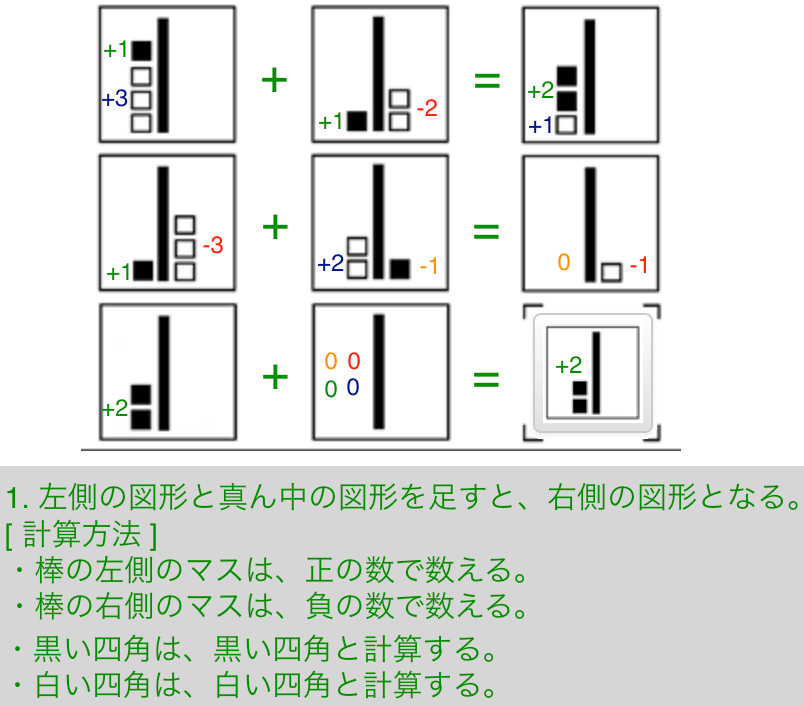
解説
- 左側の図形と真ん中の図形を足すと、右側の図形となる。
- [ 計算方法 ] 棒の左側のマスは、正の数で数える。
- [ 計算方法 ] 棒の右側のマスは、負の数で数える。
- [ 計算方法 ] 黒い四角は、黒い四角と計算する。
- [ 計算方法 ] 白い四角は、白い四角と計算する。
Exercise 30
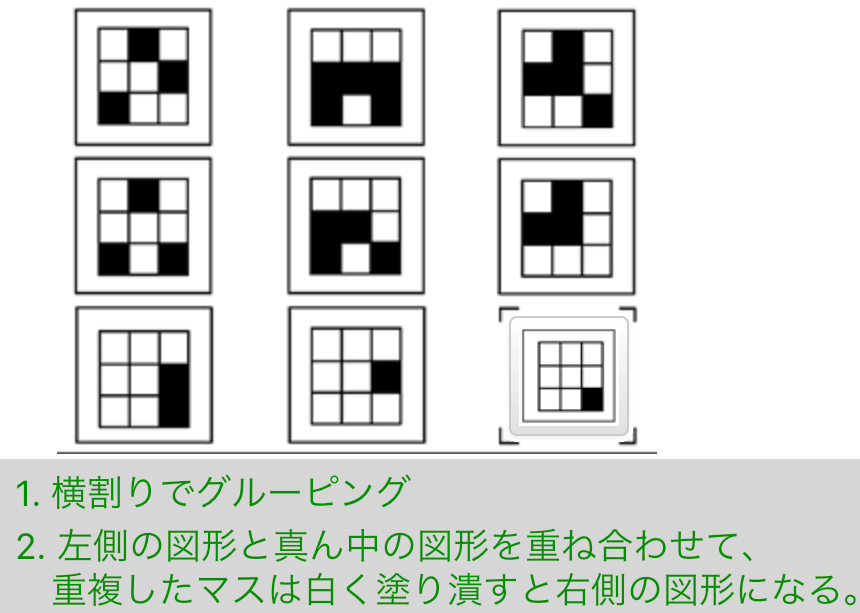
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、重複したマスは白く塗り潰すと右側の図形になる。
Exercise 31
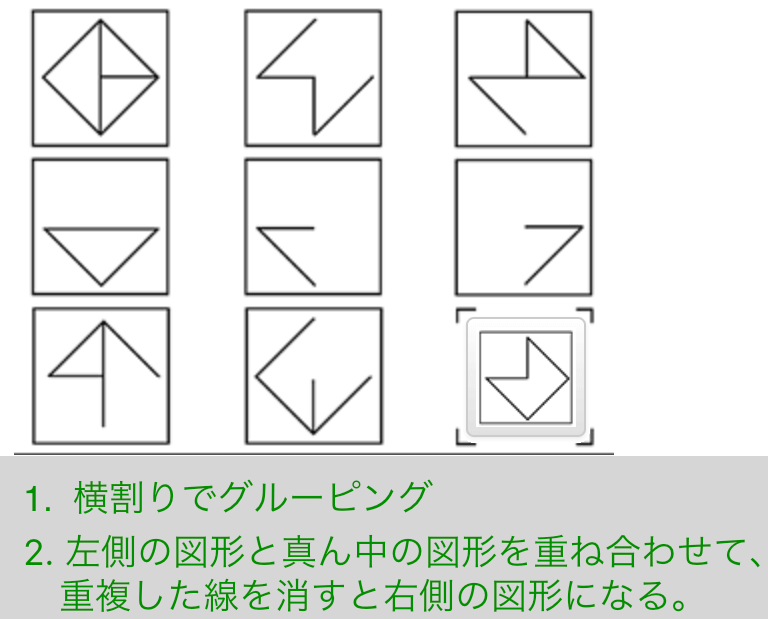
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を重ね合わせて、 重複した線を消すと右側の図形になる。
Exercise 32
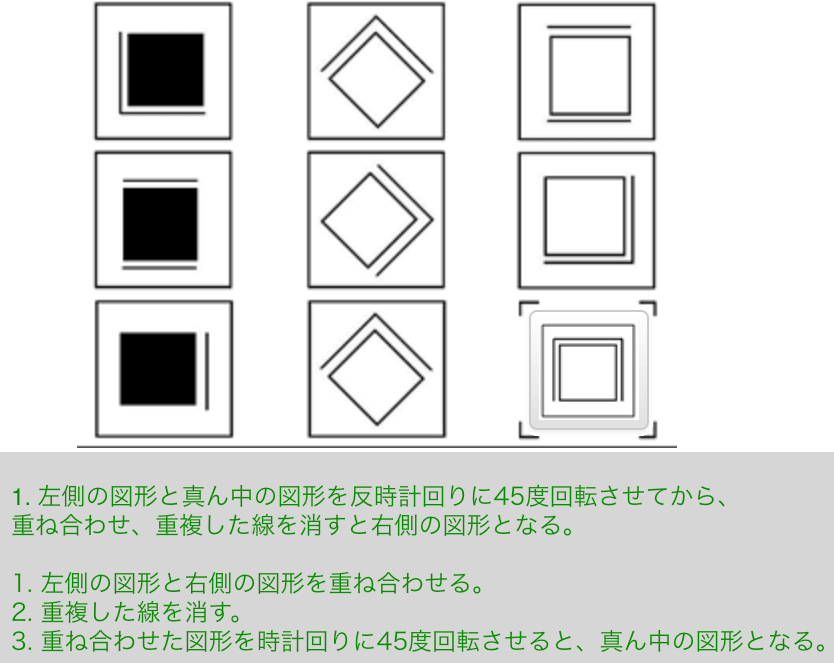
解説その1
- 左側の図形と真ん中の図形を反時計回りに45度回転させてから、重ね合わせ、重複した線を消すと右側の図形となる。
解説その2
- 左側の図形と右側の図形を重ね合わせる。
- 重複した線を消す。
- 重ね合わせた図形を時計回りに45度回転させると、真ん中の図形となる。
Exercise 33
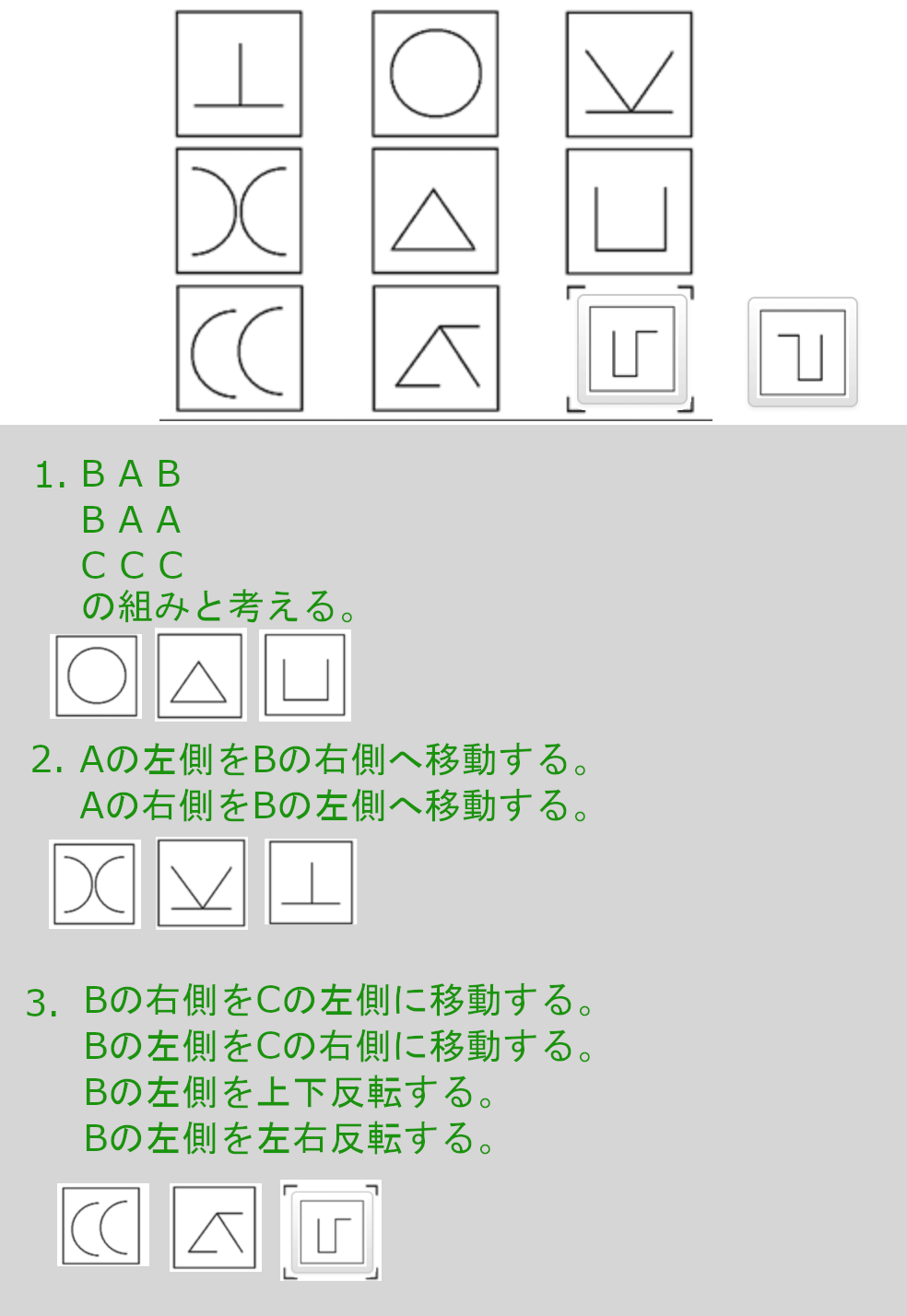
新:解説
- B A B
B A A
C C C の組みと考える。 - Aの左側をBの右側へ移動する。
Aの右側をBの左側へ移動する。 - Bの右側をCの左側に移動する。
Bの左側を上下反転する。
Bの左側を左右反転する。
Special thanks
コメント欄:[ n ]さんより
旧:解説After
- 記号の基本形は「丸:◯」「三角:△」「四角:□」の3つ
- 記号は垂直に二等分して分けて考える。
- 中段の法則 : 上段の左半分を右に動かし、上段の右半分は左に動かす。
- 下段の法則 : 中段の左右のどちらかの記号を固定する。
- 下段の法則 : 中段のもう片方の記号を水平反転してから、垂直反転させる。
- 下段の法則 : なぜ丸は右半分を固定し、三角は左半分を固定し、四角は左半分を固定するのかは不明。
Exercise 34
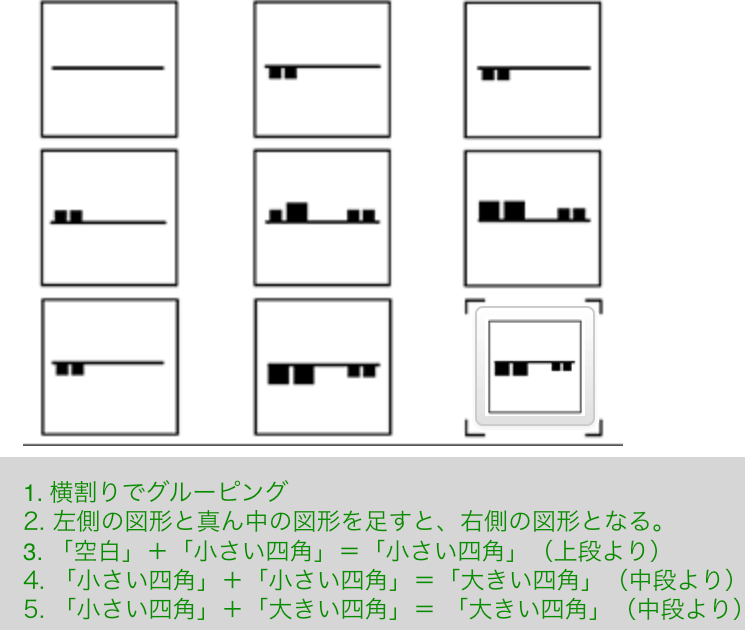
解説
- 横割りでグルーピング
- 左側の図形と真ん中の図形を足すと、右側の図形となる。
- 「空白」+「小さい四角」= 小さい四角(上段より)
- 「小さい四角」+「小さい四角」= 「大きい四角」(中段より)
- 「小さい四角」+「大きい四角」= 「大きい四角」(中段より)
Exercise 35
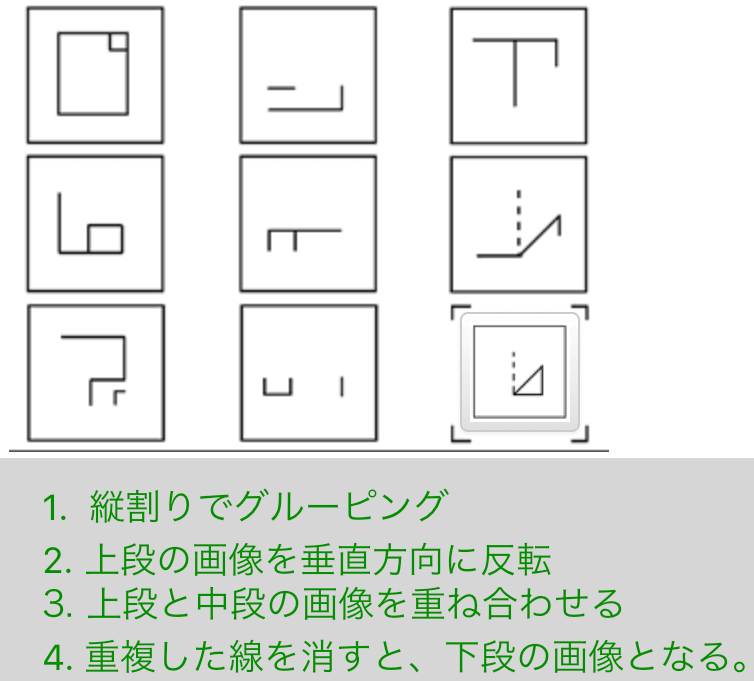
解説
- 縦割りでグルーピング
- 上段の画像を垂直方向に反転
- 垂直反転した上段と、中段の画像を重ね合わせる。
- 重複した線を消すと、下段の画像となる。
最後に
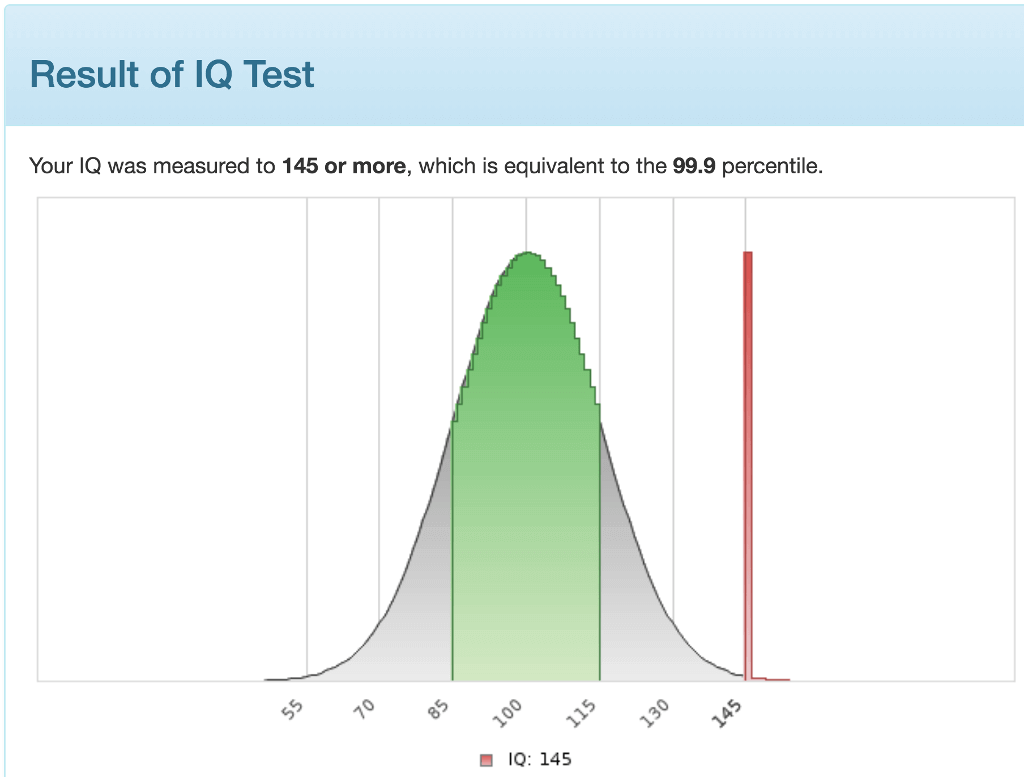
以上、ノルウェーメンサの答えでした。全問正解するとスコアが145になります。
ありがとうございました。