はじめに
この記事には『IQtest.dkの答え』が書かれています。全39問の答えと解説、さらには図解も付いています。IQtest.dkの正解だけを知りたい方は目次をご覧ください。答えの一覧があります。
IQtest.dk のURLは:こちらになります。
それでは、IQtest.dk English版の全39問の解答と解説をしていきます!
IQtest.dk 答え
第1問
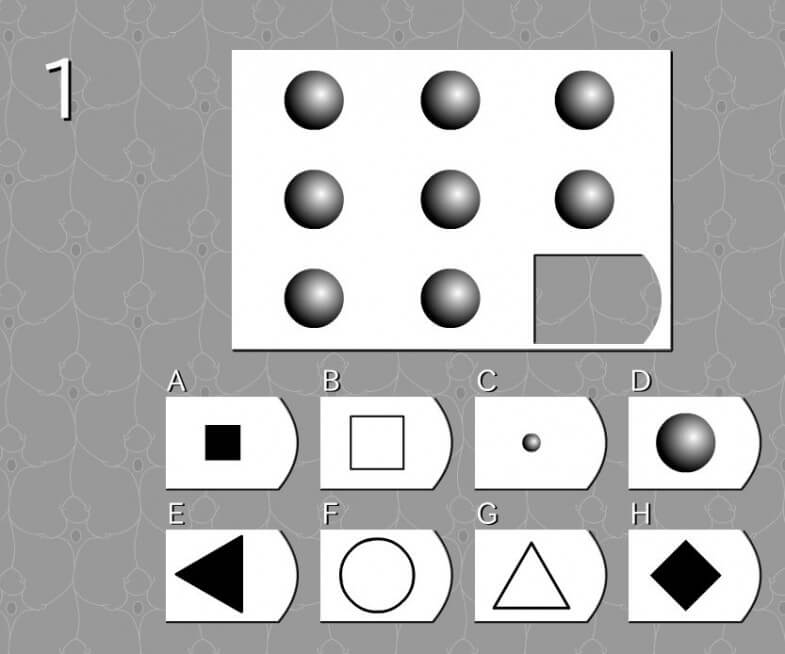
答え D
法則性
- 統一感
解説
- 上段:丸→丸→丸
- 中段:丸→丸→丸
- 下段:丸→丸→丸
第2問
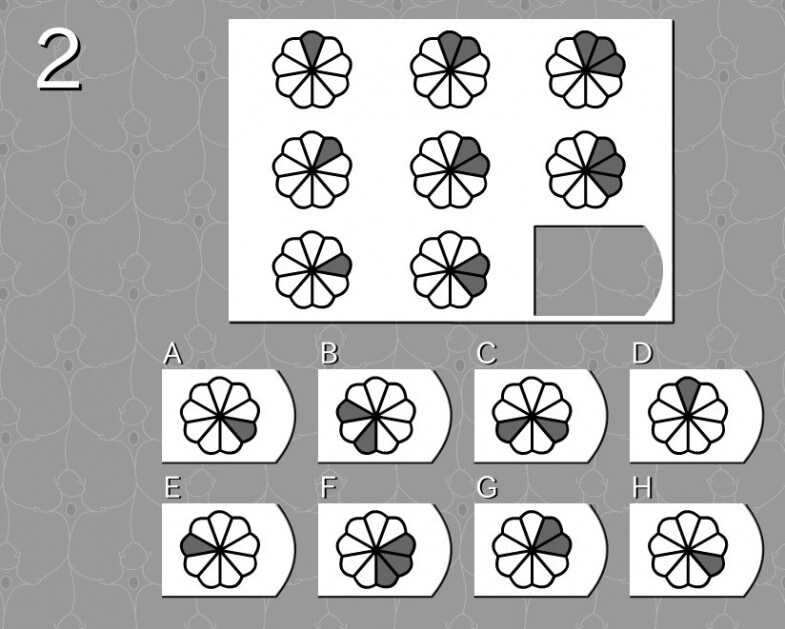
答え F
法則性
- 花びらが1枚→2枚→3枚と広がってく。
- 起点とする場所は最初に花びらがあった場所。
解説
- 上段:1を基点として→2→3
- 中段:1を基点として→2→3
- 下段:1を基点として→2→3
第3問
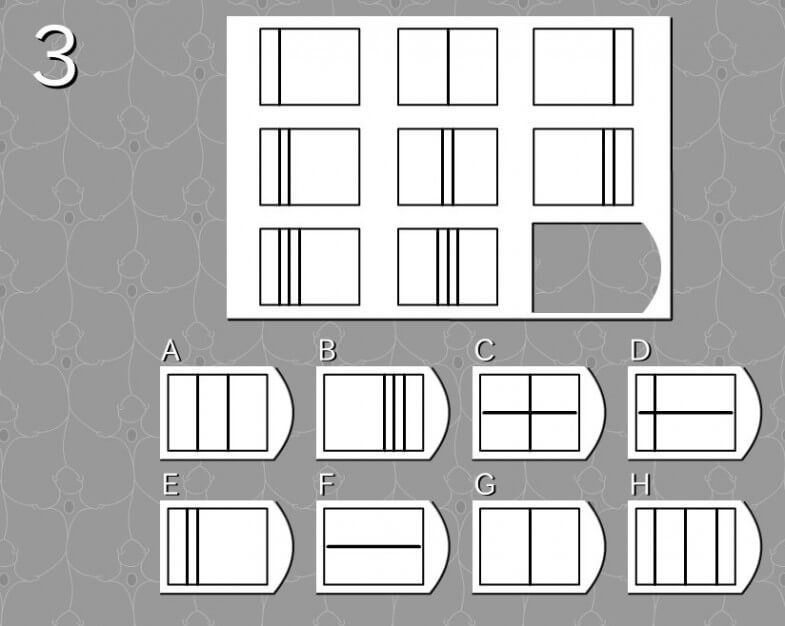
答え B
法則性
- 線の移動(左→中央→右)
解説
- 上段:一本線が左→中央→右へと移動。
- 中段:二本線が左→中央→右へと移動。
- 下段:三本線が左→中央→右へと移動。
第4問
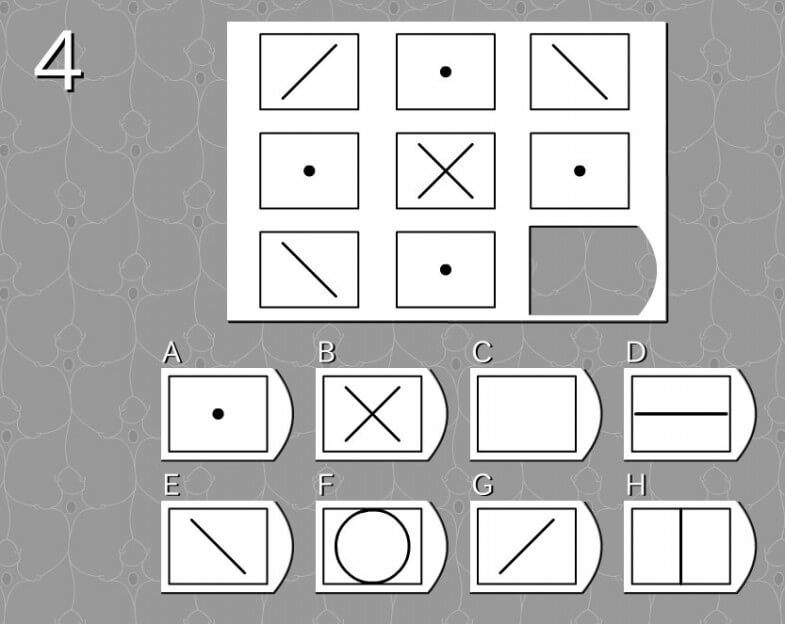
答え G
法則性
- 矛盾のない答え
- 全体性
- 上下左右対称
第5問
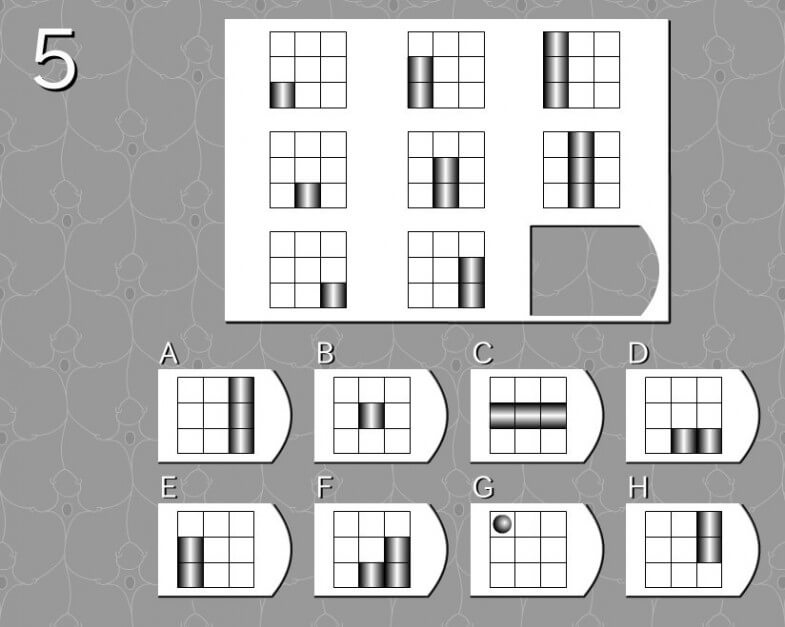
答え A
法則性
- 1マスのある部分を起点に上へ1マスずつ伸びていく
解説
- 上段:左1マス→左2マス→左3マス
- 中段:中央1マス→中央2マス→中央3マス
- 下段:右1マス→右2マス→右3マス
第6問
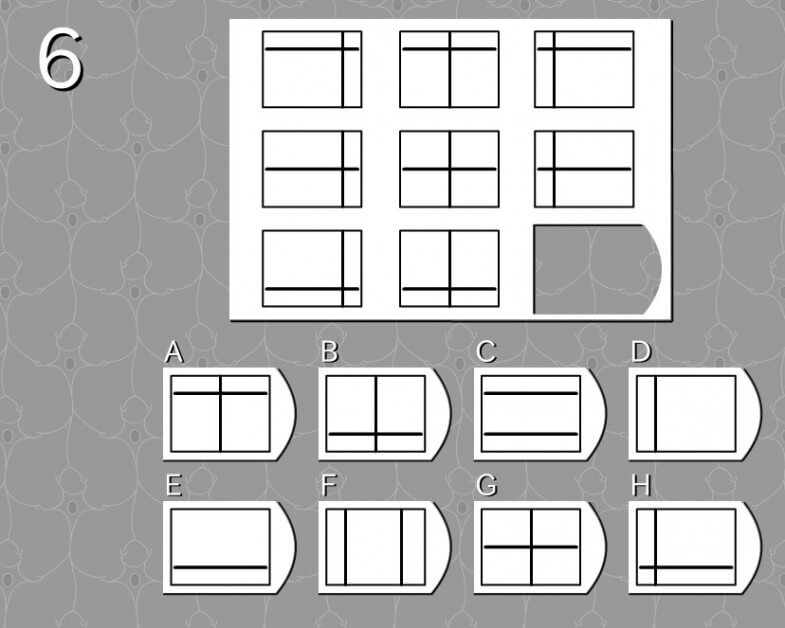
答え H
法則性
- 横棒は上段中段下段に対応
- 縦棒は左側中央右側に対応
解説
- 下段:横棒は下
- 下段:縦線は左
第7問
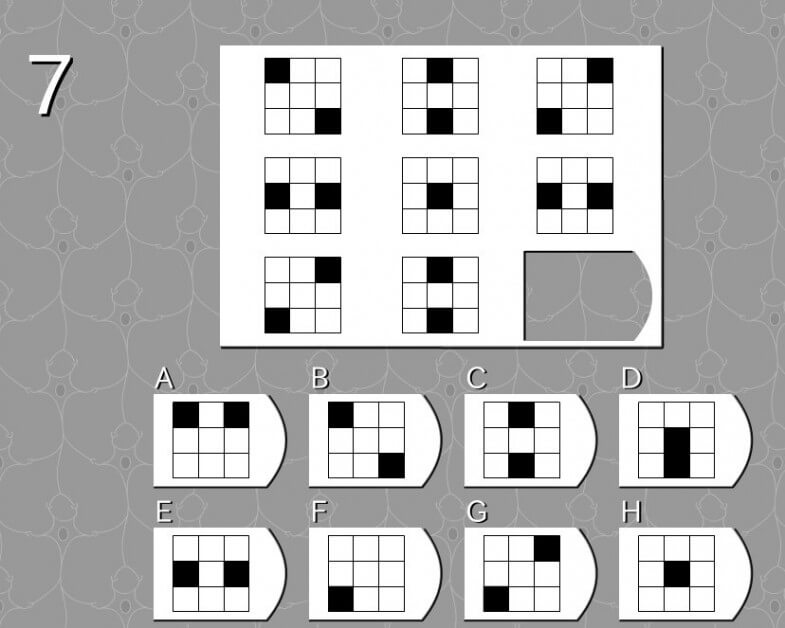
答え B
法則性
- 上側の黒マスは右へ1マスずつ移動
- 下側の黒マスは左へ1マスずつ移動
解説
- 下段:上側の黒マスは ”右”→”中央”→”左”へと移動。
- 下段:下側の黒マスは ”左”→”中央”→”右”へと移動。
第8問
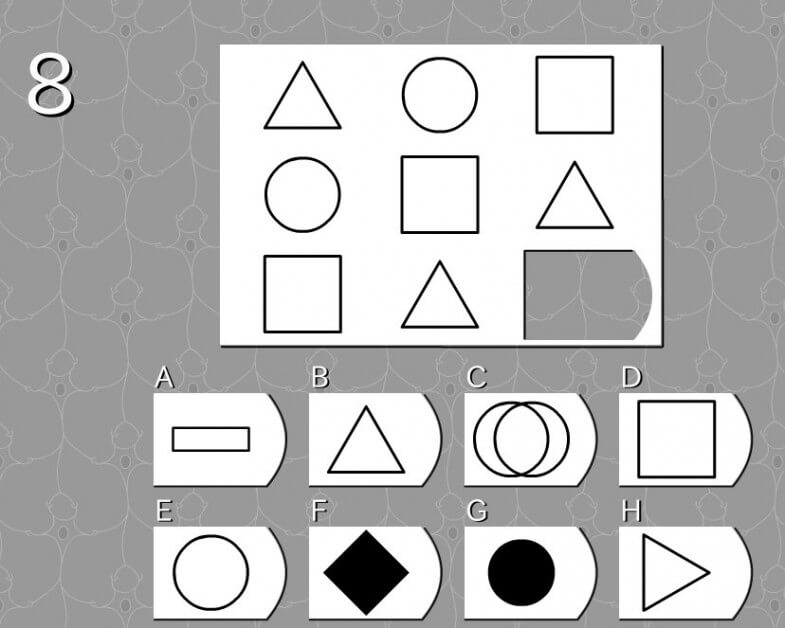
答え E
法則性
- 図形が三角→丸→四角と形を変えながら移動
解説
- 四角→三角→丸
第9問
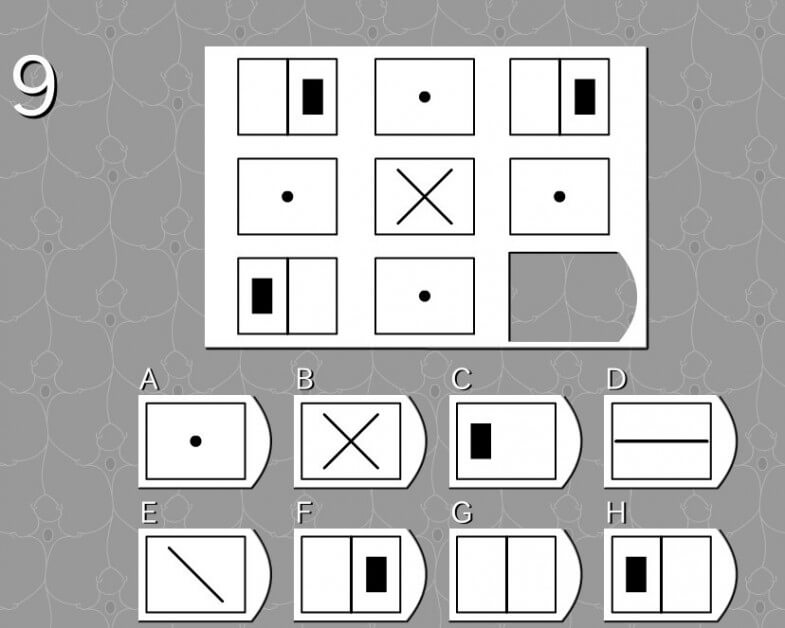
答え H
法則性
- 全体的に見て矛盾のない答え
- 統一感
解説
- 左側の図形と同じ図形
第10問
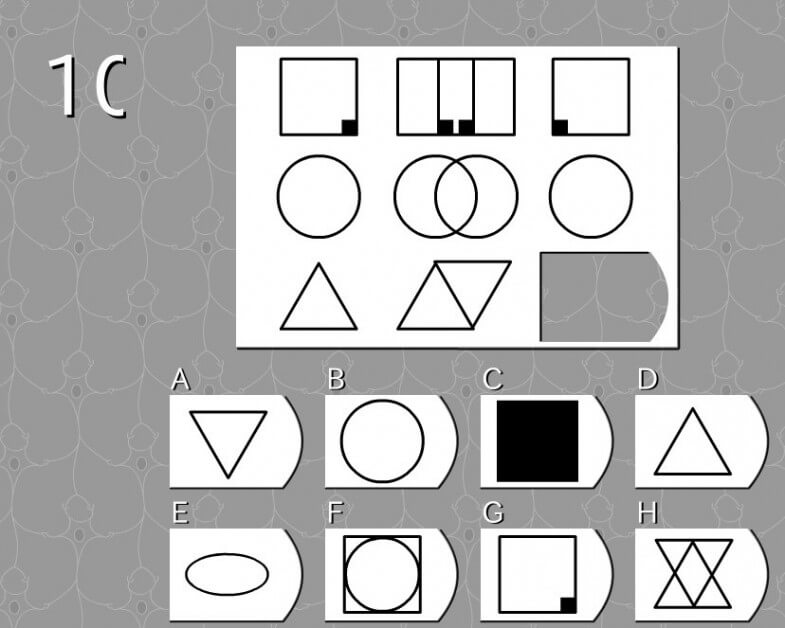
答え A
法則性
- 左側の図形と右側の図形を重ね合わさると、中央の図形になる。
- 左側の図形を中央の図形から引くと、右側の図形になる
第11問
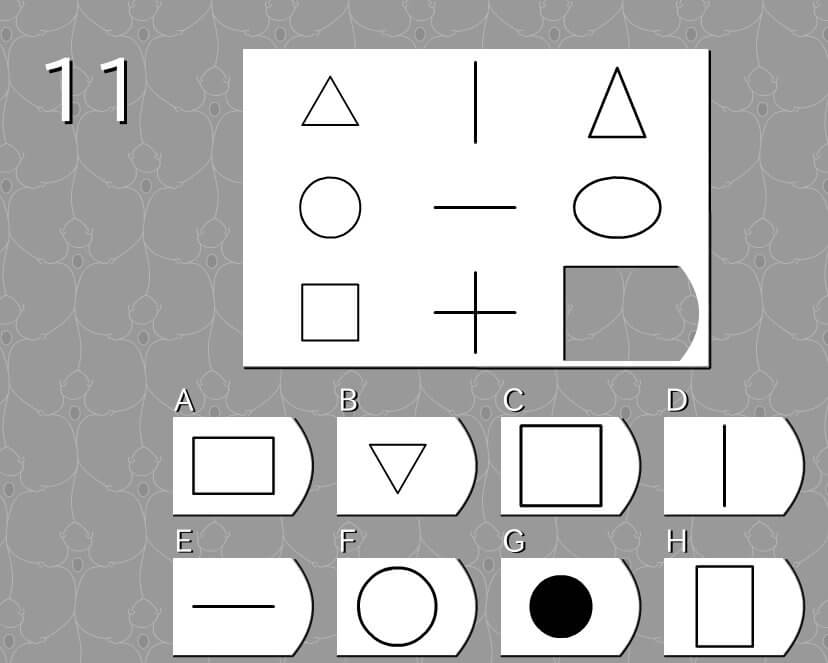
答え C
法則性
- 左側の図形を真ん中の図形方向へ伸ばすと、右側の図形となる。
- 左側の図形の長さを真ん中の図形の長さに合わせると、右側の図形となる。
解説
- 左の画像の四角形を、真ん中の画像の十字が入るように広げる。
- イメージは、左側の図形は輪ゴムのような柔らかさ、真ん中の図形はわり箸かつまようじのような硬さ。
第12問
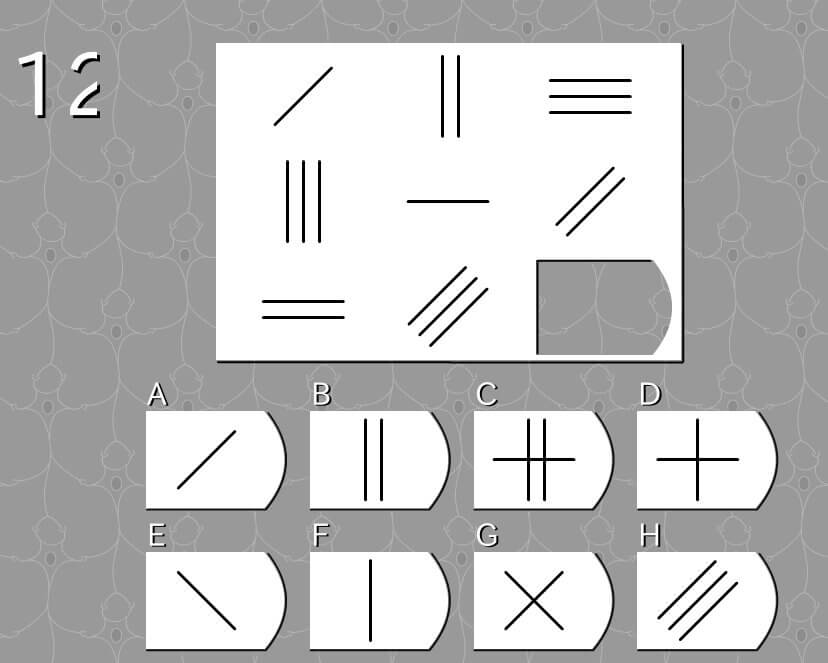
答え F
法則性
- 棒の数を増やしながら図形を回転させる
- 棒の数は1→2→3と増える
- 図形は縦→横→斜めと回転する
解説
- 下段:1本線→2本線→3本線 (候補は1本線のA,E,F)
- 下段:縦→横→斜め (候補は縦のF)
第13問
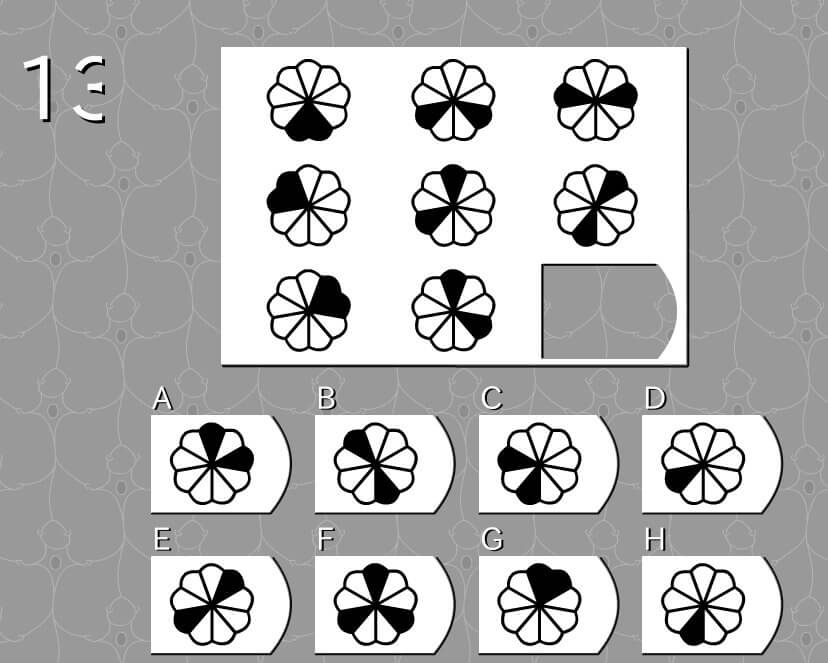
答え B
法則性
- 左側の図形を基点として、黒マスを左右に開いていく
第14問
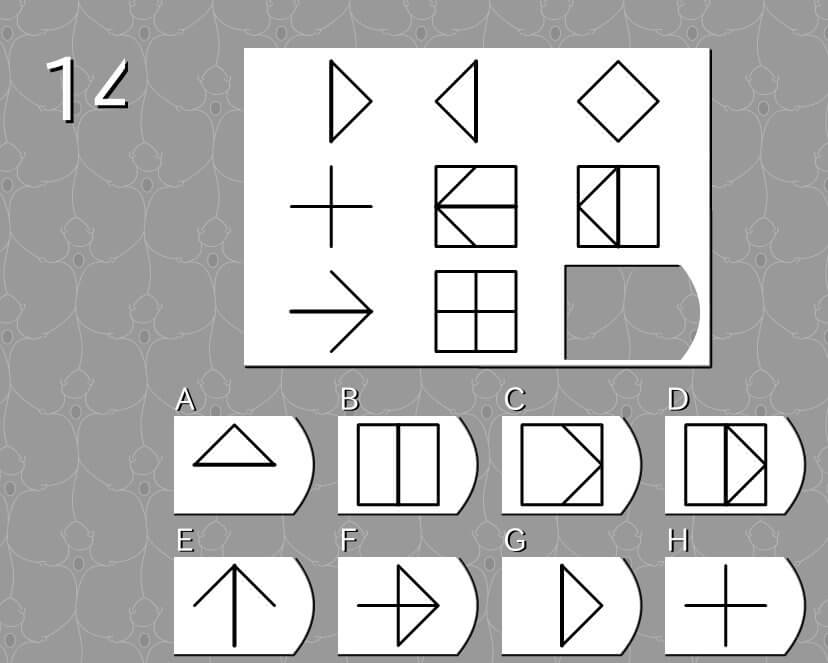
答え D
法則性
- 左側の図形と真ん中の図形を重ね合わせ、重複している線を消すと、右側の図形になる。
解説
- たとえば、上段は重ね合わせたとに重複している線は縦線だけなので、縦線を消し去った図形は菱形となる。
- 下段も、重ね合わせた後に重複している線は、中央の横線だけなので、答えはDとなる。
第15問
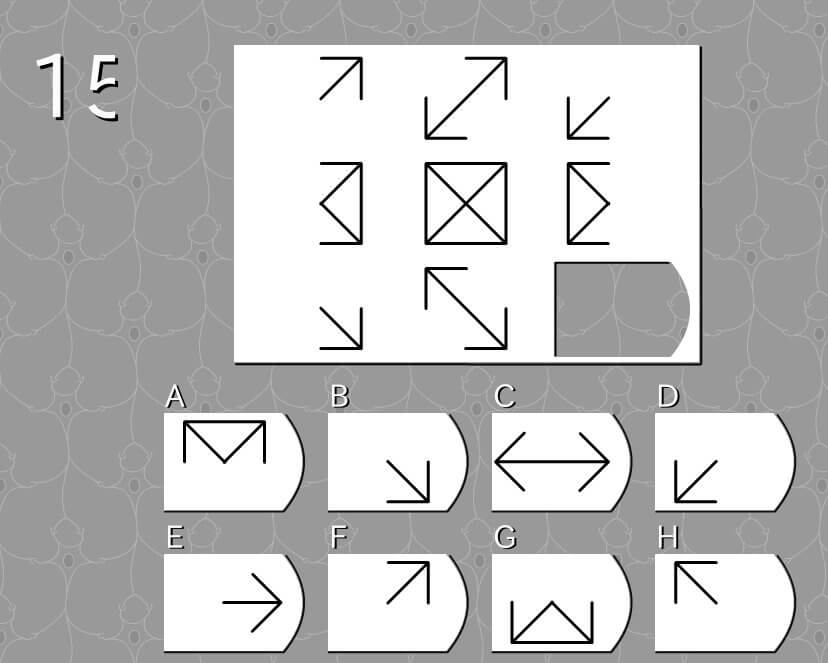
答え H
法則性
- 左右の図形を足し合わせると、真ん中の図形となる。
- 左右の図形を重ね合わせると、真ん中の図形となる。
- 真ん中の図形から左側の図形の部分を引くと、右側の図形となる。
第16問
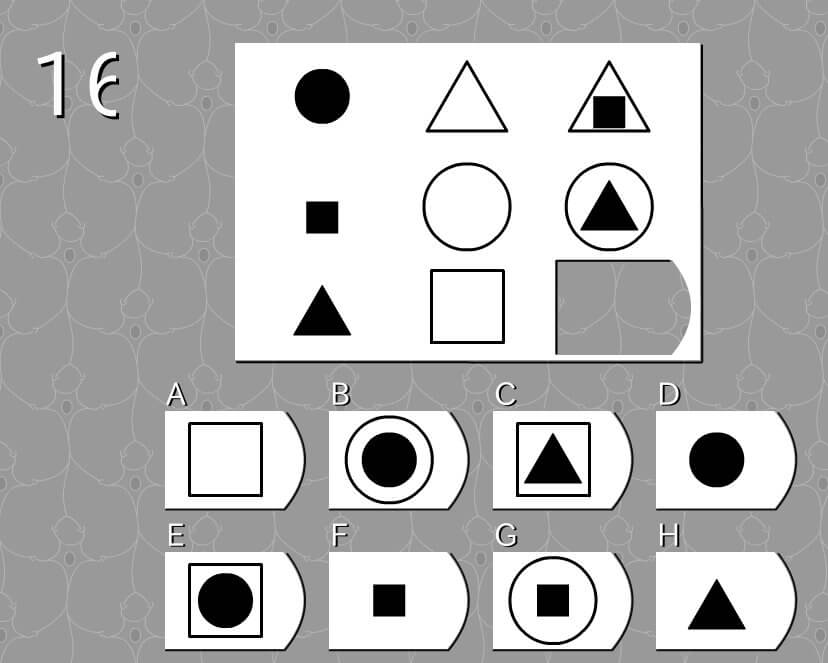
答え E
法則性
- 中央の図形に、左側の図形を丸→四角→三角→の順で変形させながら入れる。
- 中央の図形に左側の図形を変形させながら入れる。
- 左側の図形は、丸→四角→三角→の順で変形する。
解説
- 外側の囲み:三角 → 丸 → 四角(候補はA,C,E)
- 中に入れる図形:四角 → 三角 → 丸(候補はE)
第17問
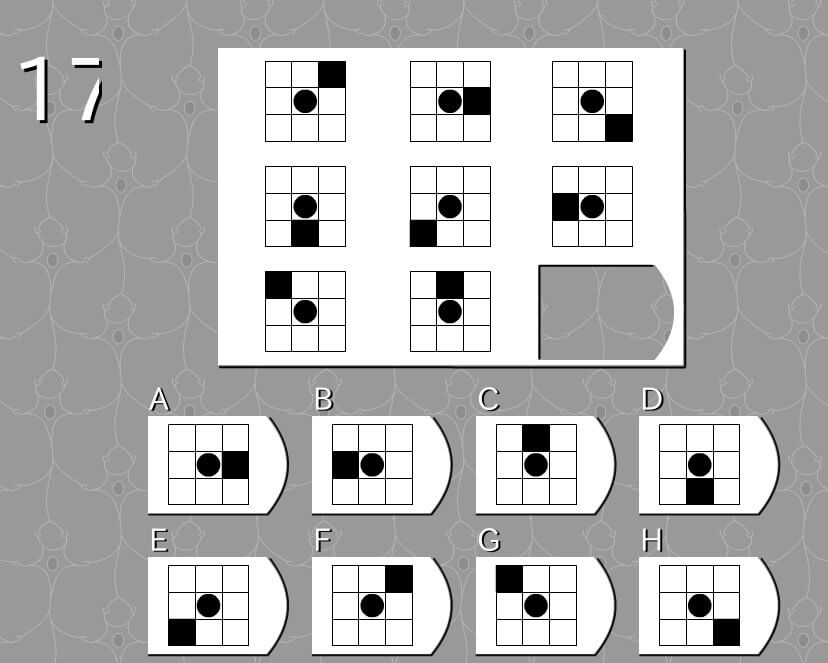
答え F
法則性
- 中央の黒丸を中心にして、黒色の四角に塗りつぶしてあるマスを、時計回りに1マスずつに移動させる。
解説
- イメージ的には太陽の周りを周回する惑星や、時計の針。
第18問
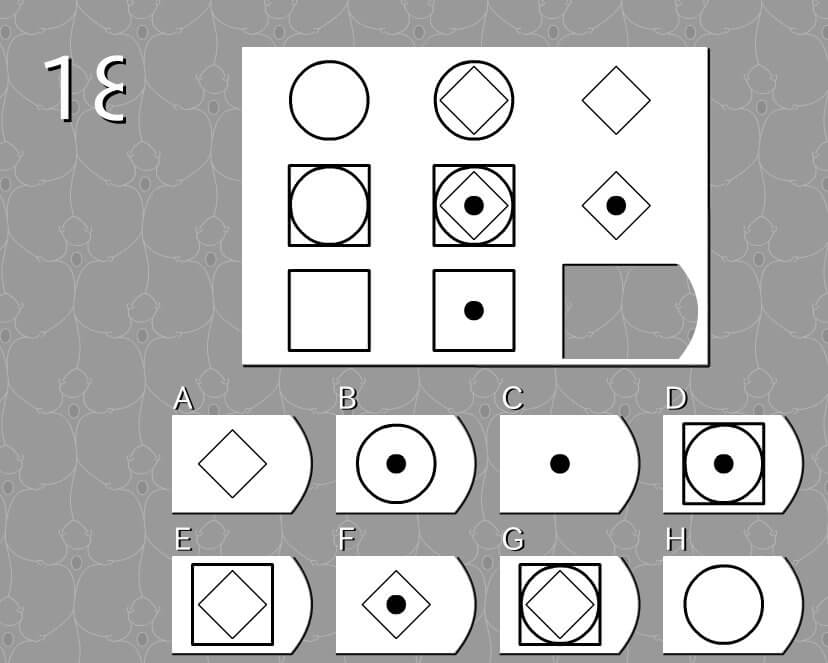
答え C
法則性
- 中央の図形を左側の図形で引くと、右側の図形となる。
- 中央の画像で左側の画像を引くと、右側の図形となる。
- 中央の画像と左側の画像を重ね合わせ、重複している部分を消すと、右側の図形となる。
解説
- 下段:左側の四角形を中央の四角形と黒丸の図形から引くと、黒丸だけとなる。
第19問
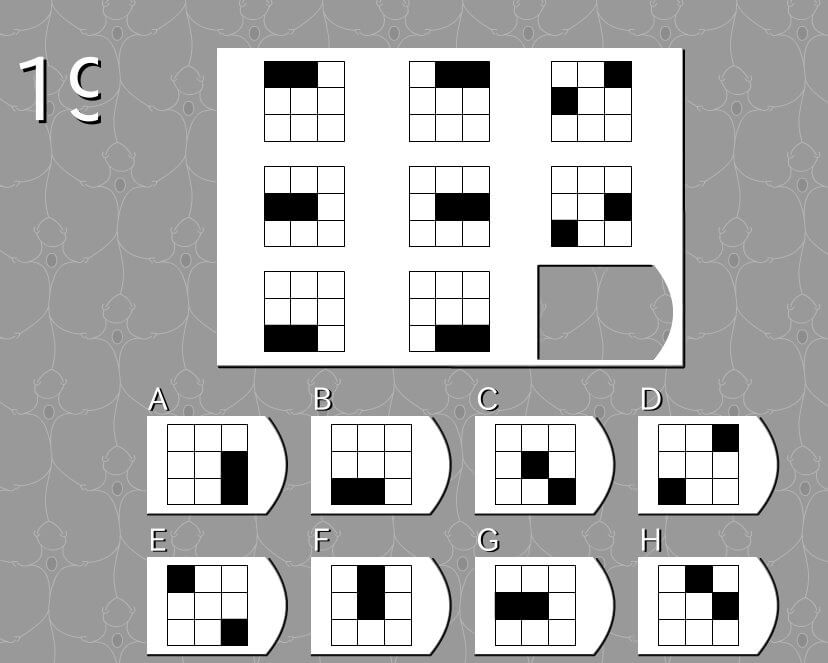
答え E
法則性
- 黒マスは1マスずつ右へ移動する
- 右端へきた黒マスは一段下げて左端へ移動する
解説
- 下段中央の黒マスは、左上から数えて8番目と9番目にある。
- 左上から数えて8番目の黒マスは、次に9番目のマスに移動する。
- 左上から数えて9番目の黒マスは次に移動すると、一段下げて左端へ移動するので、左上から数えて1番目のマスに移動する。
第20問
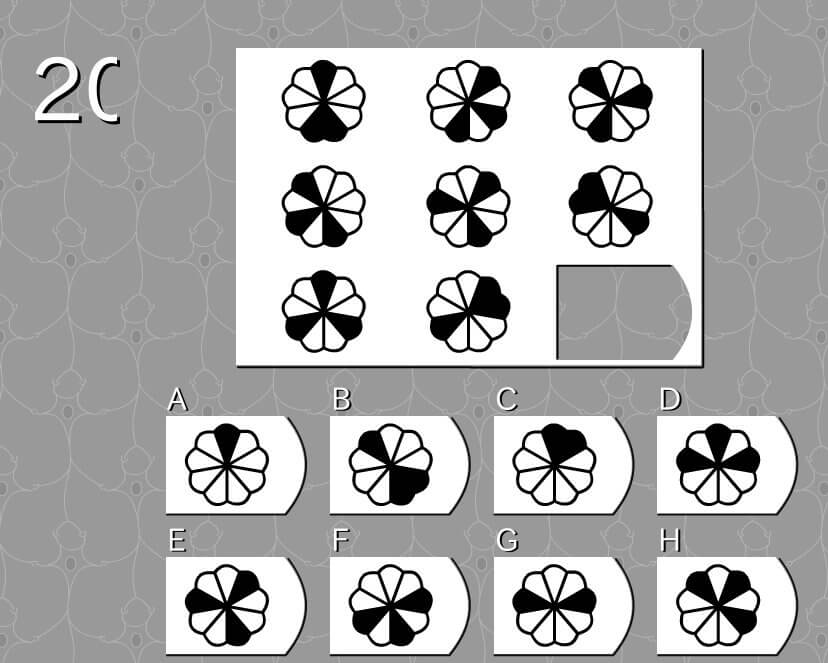
答え D
法則性その1
- 黒マスをI型・T型・Y型と分類する。
- 上中下段の同じ型別に重ね合わせると、9つのマスが全部重複なく真っ黒になる。
*コメント欄「りょん」さんより参考
法則性その2
- 黒マスをI型・T型・Y型と分類する。
- 型は、I型→T型→Y型へと変形しながら移動する。
- I型は、I型をI型の2マスある部分を下とし、下の左側一本を固定し、残り2本を一マスずつ右側へ移動させる。すると、T型となる。
解説その2
- 下段:Y型とI型が出現しているので右側はT型(候補はD、F、H)
- I型をT型へ変形させる。(候補はD)
図解
解説をイメージにするとこのような感じです。↓
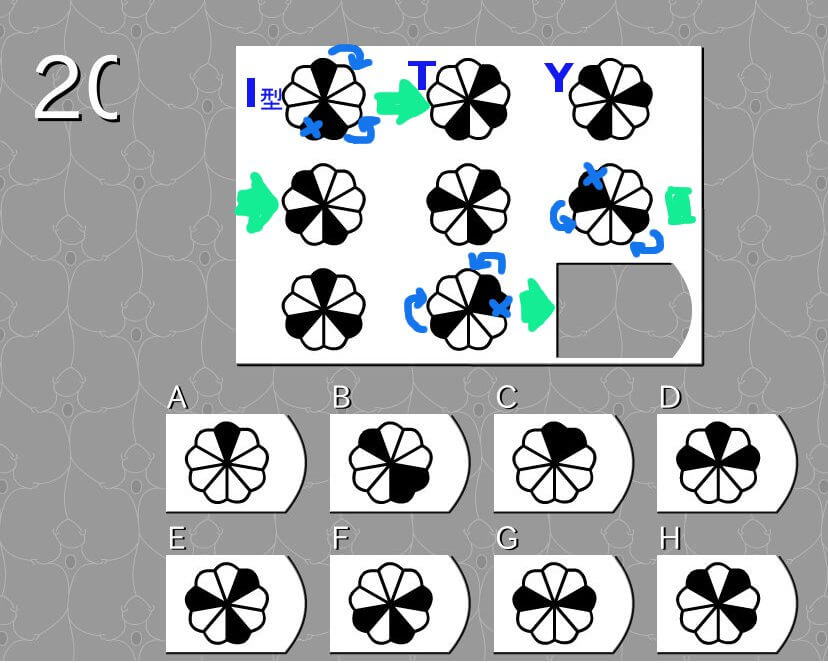
第21問
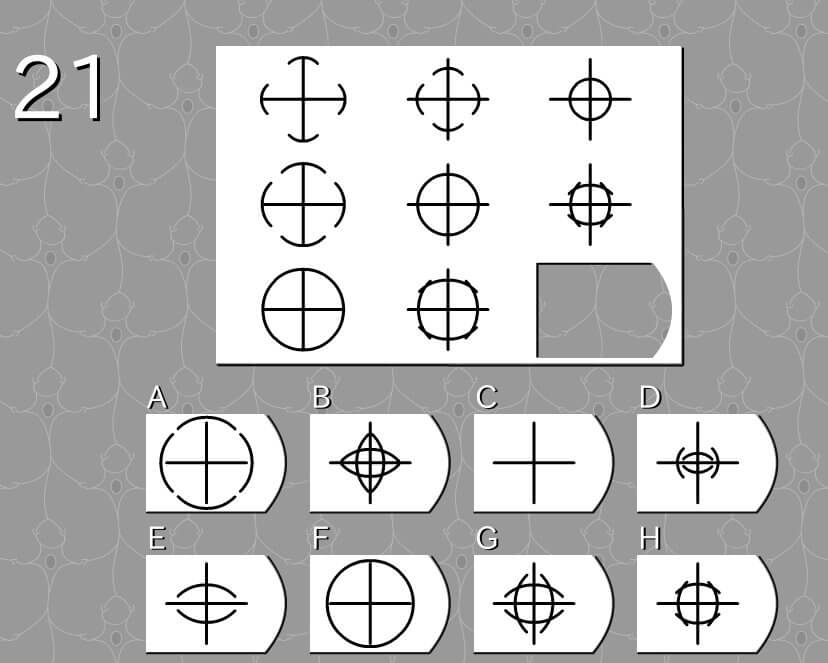
答え G
法則性
- 上下左右のカッコが中心へ移動する。
- 左側の図のカッコの位置は、一番外側の先端。
- 真ん中の図のカッコの位置は、だいたい外側2/5の位置。
- 右側の図のカッコの位置は、だいたい1/2の位置。
*カッコ=半円
解説
- カッコの位置がだいたい半分である(候補はG、H)
- カッコの長さが同じである(候補はG)
第22問
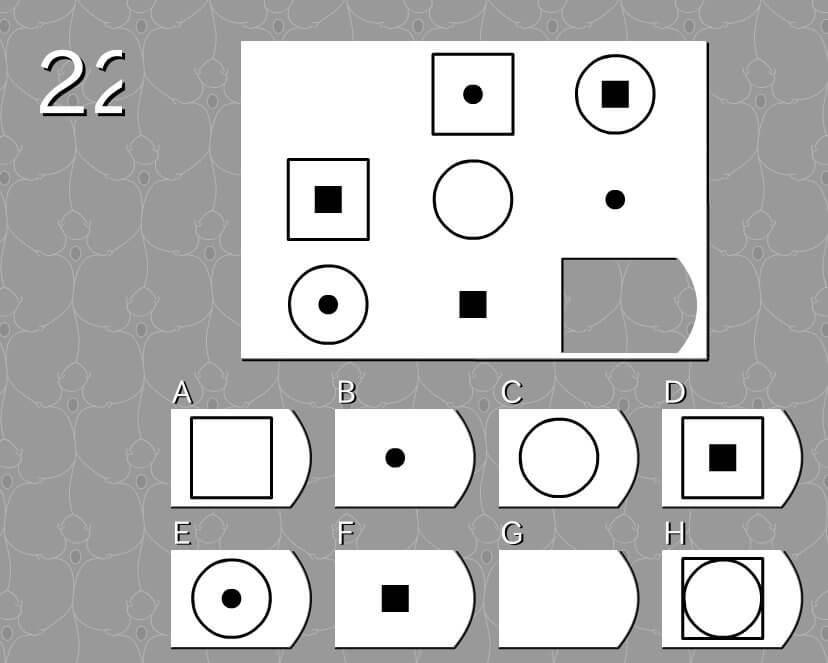
答え A
法則性
- 外枠の変化:なし → 四角 → 丸 →
- 内側の図の変化:なし → 丸 → 四角 →
解説
- 外枠の変化:丸→なし→四角(候補はA、D、H)
- 内側の図の変化:丸→四角→なし(候補はA)
第23問
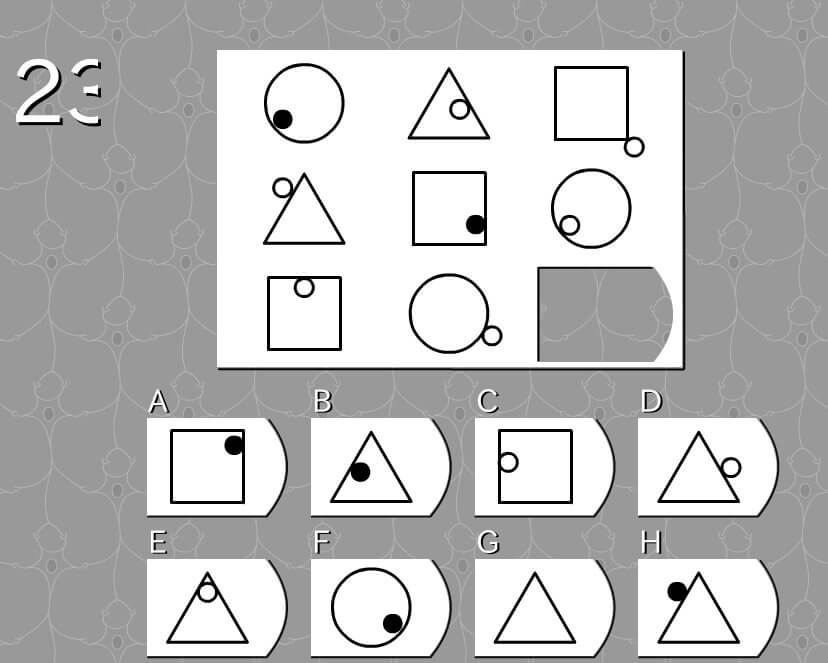
答え B
法則性
- 外側の図形は 丸 → 三角 → 四角 → の順で変形する
- 点の位置は 中 → 中 → 外 → の順で移動する
- 点の色は 黒 → 白 → 白 →の順で変色する
解説
- 図形は四角→丸→三角形(候補はB、D、E、G、H)
- 点の位置は中→外→中(候補はB、E)
- 点の色は白→白→黒(候補はB)
第24問
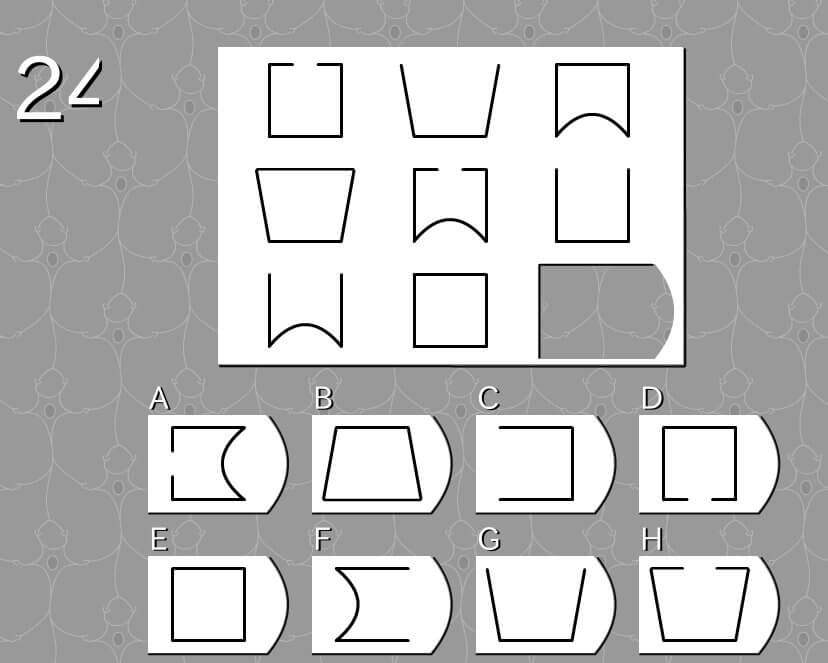
答え H
法則性
- 大まかな全体の形の変化:四角 → 台形 → 凹み →
- 図形上辺の変化:真ん中穴空き → なし → 一本線 →
- 図形下辺の変化:一本線 → 一本線 → 凹み →
解説
- 大まかな全体の形の変化:凹み → 四角 → 台形(候補はB、G、H)
- 図形上辺の変化:なし → 一本線 → 真ん中穴あき(候補はH)
- 図形下辺の変化:凹み → 一本線 → 一本線(候補はH)
(法則性3番と解説3番は不要だが考え方の一例として記入)
第25問
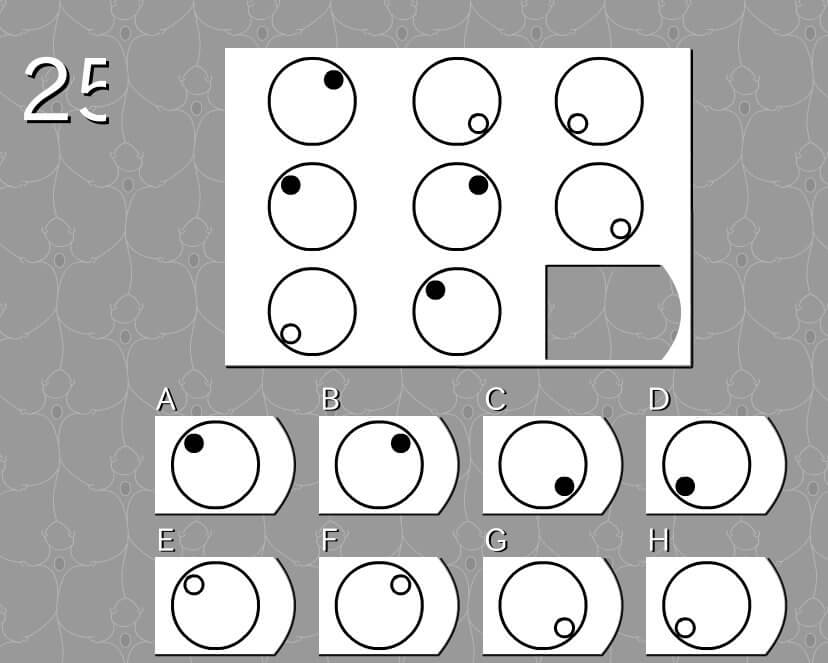
答え B
法則性
- 円形上部にある点は黒色になる
- 円形下部にある点は白色になる
- 点は右へ90°ずつ回転しながら移動する。(点は4箇所にのみ出現するため)
解説
- 点が左下→左上→右上へ移動している。(候補はB、F)
- 右上の点は円形上部にあるので、色は黒。(候補はB)
第26問
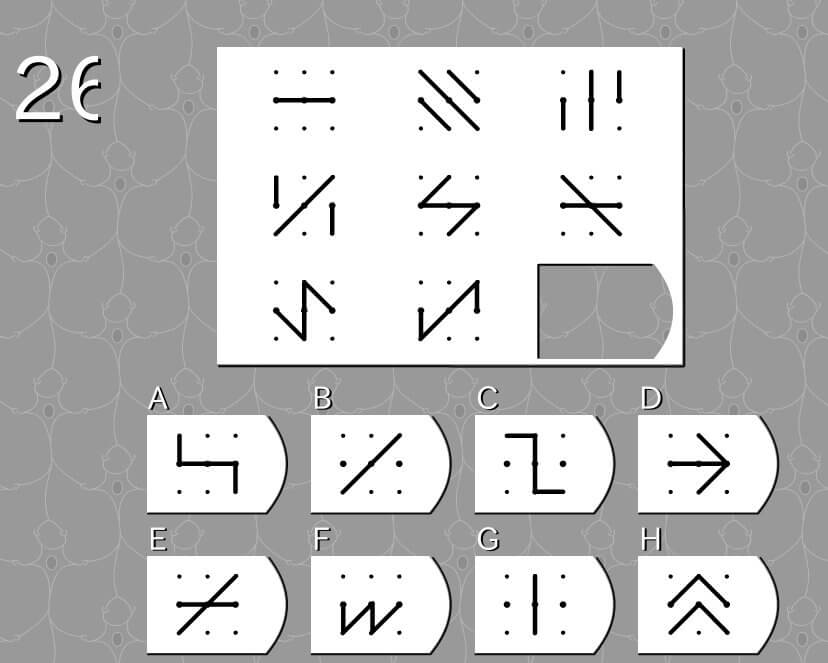
答え A
法則性
*図中の黒点を左上を1番、右上を3番、真ん中を5番、左下を7番、右下を9番と呼ぶ。
- 5番を中心にする長い棒線は、右回転する。
- 4番と6番を起点とする短い線は、右回転する。
解説
- 下段真ん中の長い線は、下段右側へ移動したとき、4番5番6番の上をなぞる線になることが推測できる。
- 6番を起点とする短い線は、上段右側から中段左側へ移動する際、黒点に制限されることなく180度動いたので、同じように6番を起点として180度回転し、6番と9番を繋ぐ線になることが推測される。
- 同じように4番を起点とする短い線は、4番と1番を繋ぐ線になることが推測される。
- よって答えはAと推測できる。
第27問

答え H
法則性
- 左側の図形と中央の図形を重ね合わせ、重複する線を消すと右側の図形となる。
- 左側の図形と中央の図形を重ね合わせ、重複する部分を消すと右側の図形となる。
解説
- 重複する部分は右下へ下がる斜めの線なので、それを消す。
- 下側横線を真ん中の図形に付け加える。
- できる図形はH
第28問

答え G
法則性
- 外側の図形は 四角 → 丸 → なし → の順で変形している。
- 中側の図形は 菱形 → 丸 → 十字 → の順で変形している。
解説
- 外側の図形は、なし→四角→丸(候補はB、G)
- 内側の図形は、丸→十字→菱型(候補はG)
第29問

答え E
法則性
- 左側の図形を真ん中の形で成形すると、右側の図形となる。
- 左側の図形の全辺を真ん中の図形の辺にすると、右側の図形となる。
- 真ん中の図形を下辺として左側の図形をくり抜くと右側の図形となる。
解説
- 図形のうねりが判りづらい場合は、うねりの両端で線を引くと単純化できてわかりやすいです。
↓こんな感じです。

第30問

答え A
法則性
- 左側の図形の内側の線へ真ん中の図形を当て込めると、右側の図形となる。
- 真ん中の図形を左側の図形の内側に収まるように縮小しながら重ねると、右側の図形となる。
第31問
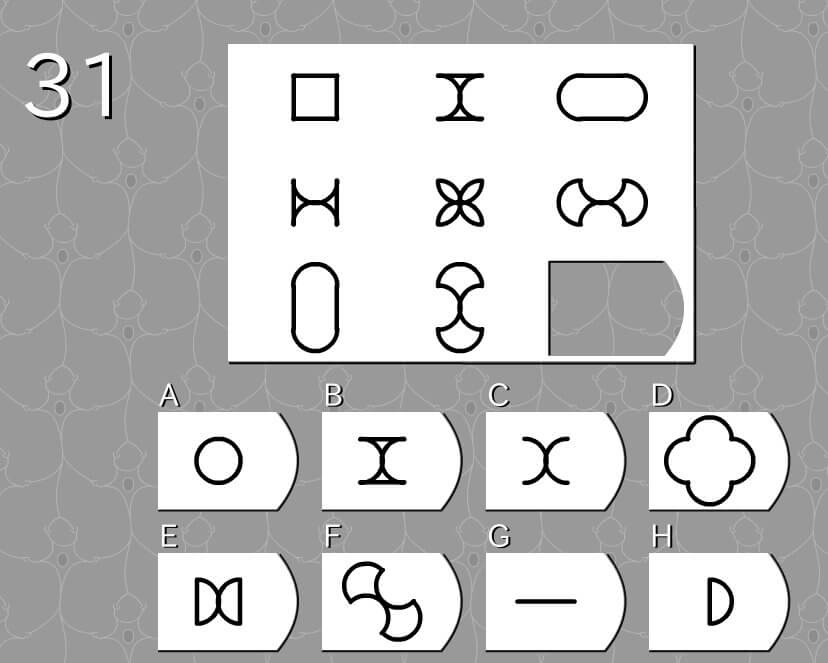
答え D
法則性
- 真ん中の図形の左右の辺を外側へ開くと、右側の図形となる。
- 真ん中の図形の左右の辺を観音開きすると、右側の図形となる。
- 左右の辺の図形変化は、直線→半円状に凹む→半円状に凸る。
第32問

答え E
法則性
- 90度動いた棒と水平に重なりあった棒が90度右へ回転する
解説
- 左側の図形の右下の棒が動く
- 動いた棒と重なり合う左上の棒を回転させる
- 〒が傾いたような形となる。
- よって答えはE
第33問

答え G
法則性
- 図形の形の変化: 波 → 8字 → 波 →
- 図形の角度変化:縦 → 横 → 斜め →
解説
- 図形の角度変化は 横 → 斜め → 縦(候補はD、G)
- 図形の形の変化は 波 → 波 → 8字 (候補はG)
- 図形の脳内操作が難しい場合、Q29でやったように線の両端を線で結ぶことで、形を簡略化でき操作もし易くなるかと思います。
第34問
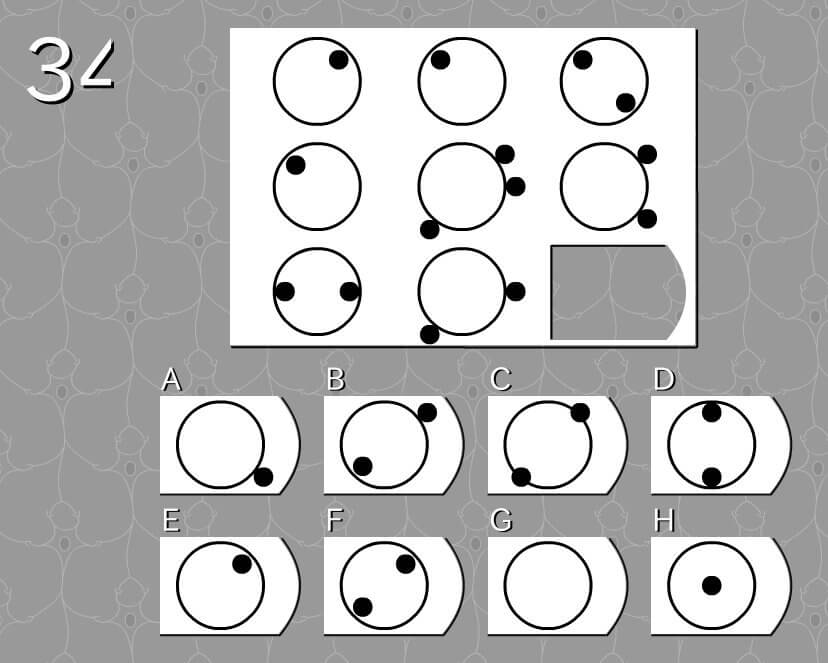
答え G
法則性
- 内側の黒点を「+」とする。
- 外側の黒点を「—」とする。
- 左側の図形と真ん中の図形を足すと右側の図形となる。
解説
- 上段:1+1=2
- 中段:1+(-3)= -2
- 下段:2+(-2)= 0
別解
- 左側の図形を水平方向に180度回転させる。
- 水平方向に180度回転させた左側の図形を、真ん中の図形と重ね合わせる。
- 黒丸が重ね合わさった場合、その黒丸を消す。
- 黒丸が円周を挟んで隣り合った場合、その両方の黒丸を消す。
- 黒丸が消えたら、真ん中の図形の中で一番下側の黒丸だけを時計回りに15度回転させる。
- もしも5. の操作で黒丸が消えたなら、もう一度3.から5. の操作を行う。
第35問
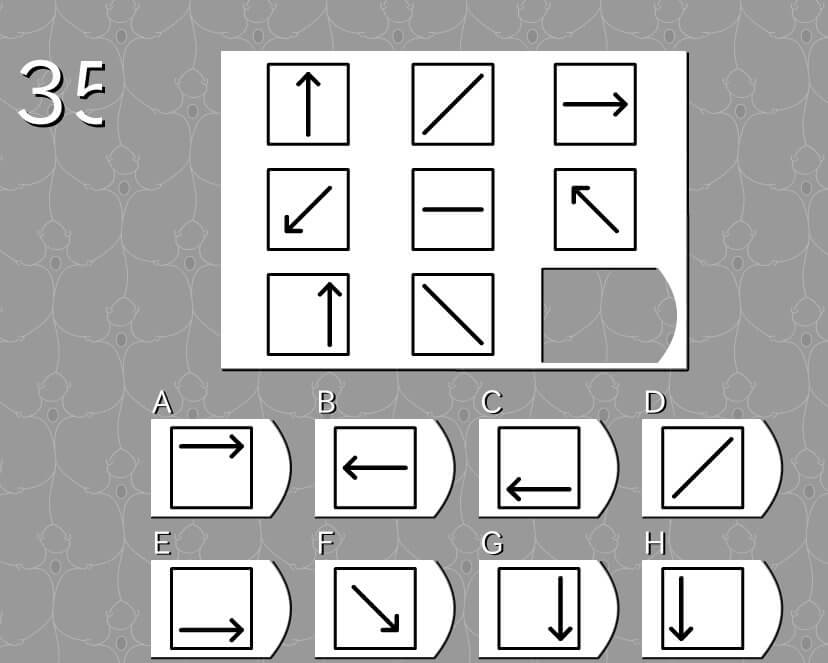
答え C
法則性
- 左側の図形を真ん中の図形の線で折り紙のように折り込むと、右側の図形となる。
- 左側の図形を真ん中の図形の線を軸として回転させると、右側の図形となる。
解説
- 物理的イメージを用いて操作するのなら、左側の図形を透明な紙にマジックで書いた矢印、真ん中の図形を厚紙に貼り付けた太い針金とし、二つの紙を張り合わせ、針金を軸にくるくると回すことで操作感を得られると思います。
第36問
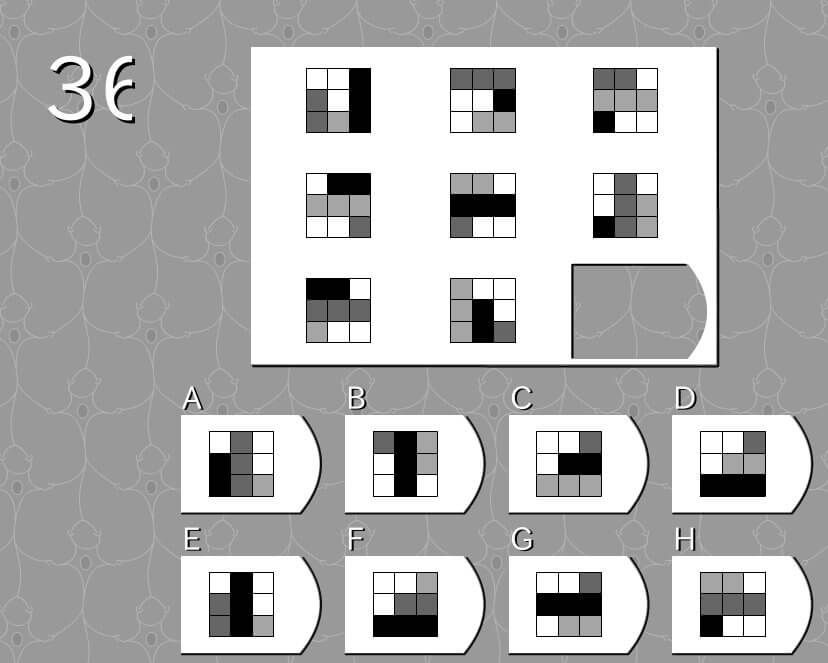
答え F
法則性その1
- 各図形を白地に書かれた棒グラフと見ると、各図のグラフは 下 → 右 → 左 → の順で底が移動する。
- 色の配色は、311、322、321の組み合わせで表れる。(数字は使われる回数)
解説その1
- 黒色:上段311、中段231、下段22X 。(311,321,322)
- 濃灰:上段232、中段113、下段31X 。(322,311,321)
- 薄灰:上段123、中段322、下段13X 。(321,322,311)
- 下段右側に来る図形は、法則性の1より、左 → 下 → 右 なので右(候補はC、D、F、G)
- 上記箇条書きにより、答えはFに絞られる。
法則性その2
- 各棒を長さが311,322、321のグループに分けると、色も対応して黒色→濃灰色→薄灰色→と変色する。
- 図を白地に書かれた棒グラフのように見る。棒グラフは下→右→左→と推移する。
解説その2
- 法則性1より:上段黒311→中段濃灰色311→下段薄灰色13X なので、Xは1と推測できる。(下段薄灰色311)
- 法則性1より:上段濃灰色232→中段薄灰色322→下段黒色22X なので、Xは3と推測できる。(下段黒色322)
- 法則性1より:上段薄灰色123→中段黒231→下段濃灰色31X なので、Xは2と推測できる。(下段濃灰色321)
- 法則性2より、答えの候補は候補はC、D、F、G。
- かつ、薄灰色の長さが1、黒色の長さが3、濃灰色の長さが2なのはFなので、答えはFとなる。
*法則性その1はコメント欄を参考に作り出した解法です。じぶんが実際に解いたときの解法は法則性その2になります。
法則性その3
- 棒グラフの向きでグループ分けして、各グループ内で棒の長さと色の関係を見る。
- 棒グラフを↑←→のグループに分ける。
- 各グループ内で、一番長い棒は黒濃淡全色ある。
一番短い棒も二番目の棒も全色ある。
解説その3
- ←グループ(候補:CDFG)
- 一番長い棒が黒(候補:FG
- 一番短い棒が淡(候補:F)
*コメント欄 A さんより引用(URL)
第37問

答え H
法則性
- 黒マスが一つずつ増殖していく。
- 白丸と黒丸が右へ1マスずつ移動している。
- 白丸と黒丸との間の距離は1マスである。 (候補は2つの丸が見えているB,H)
- 丸は黒マスから出ると色が反転する。 (候補は色が反転して白丸になっているH)
解説
- 下段左側:黒丸が2行目3列に隠れている。
- 下段中央:2行目3列に隠れていた黒丸の色が反転して2行目4列目へ。
- 下段中央:下段左側の1列3行目の黒丸が、下段中央の2列3行目の黒マスの中へ。
- 下段右側:下段中央の2列3行目の黒マスの中に隠れていた黒丸が、色を反転させて下段右側3列目3行目にあると予測できる。
- 下段右側:下段中央の2行目4列の白丸が、下段右側1列目3行目にあると予測できる。
- よって解答は、白丸が下段右側3列目3行目にあり、白丸が下段右側1列目3行目にある”H”となる。
第38問
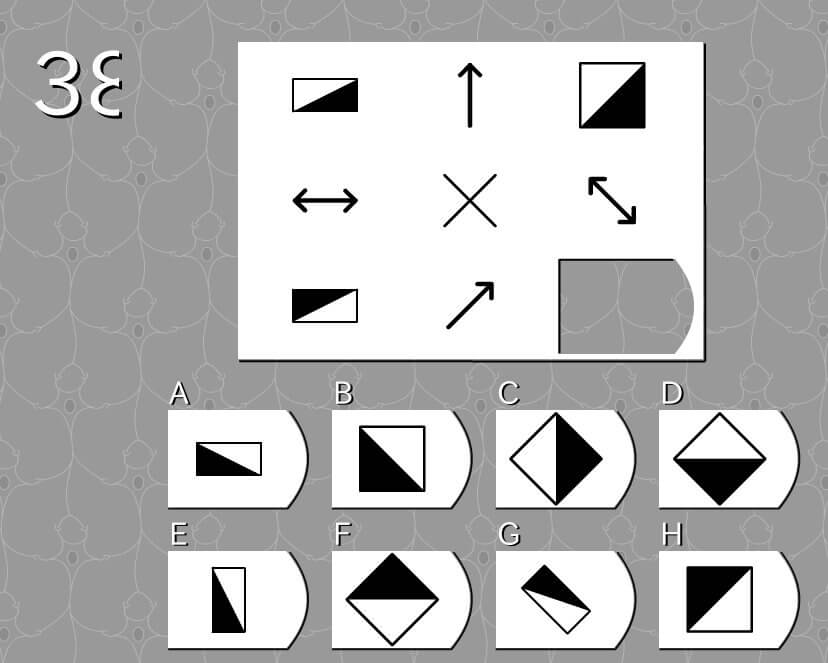
答え F
法則性
- 片矢印は図形を伸張させる長さと方向を示す。
- 両矢印は図形の向きを矢印方向と同じになるよう揃え、矢印の方向に180度回転させることを示す。
解説
- 問題を上段中段下段の横割りで捉えた場合:
真ん中の図形の片矢印の根元に、左側の図形の右下の点を固定し、矢印方向へ引っ張ると、左側の図形が伸びるので、長さと向きが変わり右側の図形となる。 - 問題を右側真ん中左側の縦割りで捉えた場合:
上段の図形を中段の両矢印の方向に向きを揃え、矢印の方向に180度回転させると、下段の図形になる。
法則その2
- 片矢印:矢印の方向に伸張
- 両矢印:90度回転
- さらに上記2つとも矢印が縦方向を向く状態を基準として傾いた角度だけ回転させる
解説その2
- 左上の図形を上に伸張したもが右上の図形
- 左下の図形を上に伸張、-45度回転したものが右下の図形
- 左上の図形を90度回転、さらに90度回転したものが左下の図形
- 右上の図形を90度回転、さらに45度回転したものが右下の図形
- 中央の×はQ4の中央にある図形みたいなもので特別な意味はないと思いました。
*コメント欄ダミーさんより全文引用(URL)
第39問

答え B
法則性
- 各記号は右へ1マスずつ移動する際に × → ○ → ▲ → の順で変化する。
解説
- 下3マスが同じ形のXXXを探す。 (候補:B,D)
- 上3マスが▲○○を探す。 (候補がB)
より詳しい解説
法則性
- 記号は右に1マスずつ移動する。
- 記号は右下に来たら左上に移動する。
- 移動するとき記号は「 × → ○ → ▲」の順で変化する。
下段中央の画像を例に解説
法則性1.で右に一マス移動させる。
X X ◯
◯ X ▲
▲ ▲◯ は 右に一マス移動して、
◯ X X
◯ ◯ X
▲ ▲▲ になる。
法則性3.で記号を「 × → ○ → ▲」の順で変化させて。
◯ X X
◯ ◯ X
▲ ▲ ▲ は
▲ ◯ ◯
▲ ▲ ◯
X X X になる。
昔の解説
- 移動の際、記号はバツ→丸→三角形の順で変形する。
- 各マスの記号は右へ1マスずつ移動する。
- A~Hの解答欄から正しい答えを探るため、下段中央の図形を見る。ちょうど左上から6番目と7番目と8番目が連続して三角形である。
- ここに注目し、つぎに1マス移動する際に変形する記号はバツである。
- よって、下辺全て、7番8番9番が バツ となる図形を探す。(候補はB、D)
- 下段中央の左上から9番目と2番目と3番目の記号は丸、バツ、バツである。ので、1マス移動すると、三角形、丸、丸となる。(候補はB)
おわりに
以上、IQtest.dk English版 全39問 解答と解説でした!
この記事は2012年4月17日に書かれたものですが、3年ぶりに記事全文を書き直しました。書き直し前と比べスッキリ見やすくなったと思います!
参考にしてみたください!
ありがとうございました。

36の解説がまったく意味が分からないのですが、、、こじつけではないですか。
正しい回答は、三つのグループに分けるという事です。
図の意味は棒グラフです。棒グラフが左から始まるグループと、右から始まるグループと、下から始まるグループの三つがあります。
消去法で、回答に該当するのは右から始まるグループなので、候補はC,D,F,Gに絞られます。
あとは色の配置が被ってないかを見て、被ってないのはFだけなのでFが正解です。
これ以上論理的に妥当な回答があるとは思えません。
3 さんコメントをありがとう。
とても美しい解答だと思います。
全員がコメント欄見るわけでもないので「美しい回答です。」とか誤魔化さないでさっさと負けを認めて36の解説修正したほうがよいでは?
下右左の3種類のグラフに分けて
黒1・2・3
濃灰1・2・3
薄灰1・2・3
のすべてを揃えるという法則性のものFが選ばれる
はよ変えろは
親切に解説を書いてくれている人に対して
1つ気に入らない解説があったからといって
「負け」などという言葉遣いで指摘する
立場ではないでしょう。
気になるならば、あなたが自分のサイトに書きなさい。
書かないならば、負けなどという失礼な言葉を使うべきではないです。
解説が分かりやすかったです。
ありがとうございます。
39についての解説で、それぞれの左側に現れる縦3マスは、
一つ前の右側縦3マスを一つ下にずらし、解説どおりの変化を加えたように思えます。
この情報がなくても、十分に回答できることとは思いましたが、解説だけでは解読できなかったので、意見させて頂きました。
コメントありがとうございます。
本日2014.7.15,加筆修正致しました。
テンキーの画像、数字の配置が逆ですよ
nyu さん
ご指摘ありがとうございます。
対象画像を削除し、新たな画像を作成し、すり替えました。
iqtest.dkの解答を探してこのサイトに辿り付きました。
とても参考になりました。ありがとうございます。
39の解答ですが、
図形が左→真ん中→右に移動するに従って、
①一つずつ右の列にずれる
②その際○→▲→×→○と変化する
③最後に左の列の図形を一つずつ下にスライドする
で全て説明できると思います。
と、思ったら7の方のコメントで法則は全て明らかになってましたね。
まあ解答をまとめるとこんなところかと。
karashiさんコメントありがとうございます。
確かにわかりずらいですね。紛らわしい書き方で申し訳ありません。
なぜ私が候補をB,Dに絞ったのかが、文章を読んで解ればこのようなコメントは頂かないと思います。
同じことをお二方にもご指摘を受けたので、私の書き方が甘かったと思う所存です。
その点を踏まえて法則性をより具体的に明記し、問39の解説を改めさせて頂きました。
訂正部分:
1.追加:→”×”→”○”→”▲”の順で変化する。
2.修正元:右へ1マスずつ移動するごとに 修正後:右へ1マスずつ移動する際に
3.追加:マスの移動は7→8→9→4→5→6→1→2→3と続く。(問37で出題した法則性と同じ。)
4.変更:ページ上部、「図中の位置の呼び方」と「箇条書きについて」を太字に変更
再追加:
1.絵の追加
ご指摘ありがとうございます。ご指摘の点を踏まえて記事を修正させて頂きました。
お前は日本人をやめろ! くだらない下等民族なんだから
はじめまして。
IQテストの結果、36問目以外は全て正解出来ました。
しかし36問目だけは、解説および他の方のコメントを見てもどうしても理解出来ないので、もう少し詳しく教えてもらえますか?
右側から伸びる棒グラフになるはずだ、(候補はC,D,F,G)というところまでは容易ですが、
そのあとの絞り込みが理解出来ません。
【疑問1】
>下段の配色は、黒色22X、灰色31X、ねずみ色13X
>黒色は223のグループなので、候補はD,F,G
>黒色3マス棒を見る
↑
>黒色は223のグループなので
と当然のように突然言われていますが、
いつどこで黒色が223のグループだと説明づけられている(説明づけられる)のでしょうか?
【疑問2】
疑問1が理解出来て、黒色3マス棒がある選択しに絞ることが出来た後の解説で、
>上段の黒色3マス棒は、棒グラフの ”下”で図の右に配置されている。
>中段の黒色3マス棒は、棒グラフの ”左”で図の中央に配置されている。
>下段の黒色3マス棒は、棒グラフの ”右”で図の左に配置されていると予測できる。
↑
とありますが、そうでしょうか?
確かに、黒3マス棒の配置だけに着目すればそうですが、
では他の色の棒は?上段→中段→下段へと、「必ずしも」別の配置に変更されているわけではありません。
(例えば、濃い灰色の3マス棒は、上段(右)→中段(中央)→下段(中央)となっているし、
薄い灰色の3マス棒は上段(中央)→中段(中央)→下段(左)となっています。)
ですから、「黒3マス棒の配置」についての説明は、結果(答え)からこじつけたか、偶然当たっただけのように思えます。
何かもっと明確な法則性があるのではないでしょうか?
【疑問3】
また、他の方のコメントで、
>色の配置が被ってないかを見て、被ってないのはFだけ
↑
とありましたが、
「色の配置が被ってないか」とはどういうことでしょうか。
【疑問4】
さらに別の方のコメントで、
>黒1・2・3
>濃灰1・2・3
>薄灰1・2・3
>のすべてを揃えるという法則性のものFが選ばれる
というのも理解出来ないので(123とは何?)、
分かるようでしたら解説いただけないでしょうか。
自己レスです。
>「色の配置が被ってないか」
また、
>黒1・2・3
>濃灰1・2・3
>薄灰1・2・3
>のすべてを揃えるという法則性のものFが選ばれる
について、これかな?と思うことを発見しました。
棒の種類と本数に法則があるようです。
黒の3ブロック棒が使われた回数→2
黒の2ブロック棒が使われた回数→3
黒の1ブロック棒が使われた回数→3
濃い灰色の3ブロック棒が使われた回数→3
濃い灰色の2ブロック棒が使われた回数→2
濃い灰色の1ブロック棒が使われた回数→3
薄い灰色の3ブロック棒が使われた回数→3
薄い灰色の2ブロック棒が使われた回数→3
薄い灰色の1ブロック棒が使われた回数→2
9つの図において、これら全ての棒が、3回ずつ使われると予想すると、
問題の図には、
黒の3ブロック棒、 濃い灰色の2ブロック棒、 薄い灰色の1ブロック棒
を一回ずつ出てくることになります。
この着目点によると、解答はEかFとなり、
あとは右から伸びている棒グラフ、ということでFに絞り込めます。
いかがでしょうか。
Mさんへ
熱心なコメントありがとうございます。
たしかにMさんの法則性からも答えを導き出せますね。
自己スレされているので解決されているかもしれませんが、書き出された疑問点について答えていきます。
Q1.黒色が223のグループだと説明づけられている(説明づけられる)のでしょうか?
A1. 解説の5.6.で説明しています。
Q2. 何かもっと明確な法則性があるのではないでしょうか?
A2. 確かにあります。よりわかりやすくなるよう解説文を書き直しました。
Q3. 「色の配置が被ってないか」とはどういうことでしょうか。
A3. 他の方の見解なので私には分かりかねます。
Q4. 分かるようでしたら解説いただけないでしょうか。
A4. Q3とおなじように、他の方の見解なので私には分かりかねます。
ありがとうございました
Q20、難しく考えすぎの気がします。
単純に、T型、I型、Y型が三つずつあり、どの型も3つ重ね合わせると黒がかぶらない組み合わせになる、というだけでいいのでは。
配置にも、I-T-Yの循環が各段でずれていく形で確かに法則がありますが、単に各型がQ8のように並んでいると考えれば無視してもいいと思います。
Q31、ちょっと説明が分かりにくい気がします(正解できた人は分かるけど、分からなかった人には頭に?が浮かびそうな説明)。
左端の図形中のまっすぐな縦線二本が半円状に膨らむとし、内側に膨らめば真ん中の図形、外側に膨らめば右側の図形と考える方が自然でしょう。
Q32、これも難しく考えすぎの気がしますね。
・すべての図形は、単純に縦横2×2で並んだ4つの斜線で構成されている
\/
//
・そのうえで、単純に各段で左の図形から、右下が回転→左上が回転、の順で変形する
と考えた方が汎用性が高くてすっきりするように思いました。
Q35
折り込むとありますが、折れてはいないので、「左側の図形を真ん中の図形の線を軸として対象となる図形に置き換える」のほうが分かりやすいかも。
Q36、解説を入れ替えた後も、やっぱり正解決定までの手順を複雑にし過ぎだと思います。
存在する法則をすべて記述するなら現状でも不足ですが、正解を導く必要最低限の法則に絞るなら、前提条件1は必要ないと思います。
前提条件3は、各棒、ではなく各色の棒と書くべきですね。
そして、各段の中で3色に311,322,321を割り当てるよりも、各色ごとに、各段のグラフの長さの組み合わせを見ると、そちらも311,322,321の組み合わせになっており、そこに注目すると、より早く正解が決定します。
解き方は何通りもありますが、それを踏まえてよりスピーディな判断が可能な手順に書き直すと、
—–
法則1. 各図形を白地に書かれた棒グラフと見ると、各段、各列に左右下を底とするグラフが一つずつある。
法則2.あらゆる視点で311,322,321という組み合わせが表れる。例えば各色ごとに、縦横の列ごとに3色の長さの組み合わせみると、311,322,321が一つずつあらわれる。(例えば黒:上段311、中段231、下段22?←3、濃灰:上段232、中段113、下段31?←2)
1.よりCDFGに絞られ
2.よりFに決定する
—–
法則2.の「あらゆる視点で~」について補足すると、例えば
A縦列に注目
左列:黒322、濃灰213、薄灰131
中央:黒132、濃灰311、薄灰223
右列:黒11?、濃灰23?、薄灰32?
B横列に注目
上段:黒311、濃灰232、薄灰123
中断:黒231、濃灰113、薄灰322
下段:黒22?、濃灰31?、薄灰13?
C色に注目、縦
黒:左列322、中央132、右列11?
濃:左列213、中央311、右列23?
薄:左列131、中央223、右列32?
D色に注目、横
黒:上段311、中段231、下段22?
濃:上段232、中段113、下段31?
薄:上段123、中段322、下段13?
以上は同じ事柄を違う視点でまとめただけですが、この中で手っ取り早く?をすべて埋めるには、CかDの色に注目して各色ごとに決定する方が早いので、前述のようにしました。
Q38 、これだけは何となくすっきりしません。上段と同じように本当に引っ張るだけなら、正解の図形にはならないと思いますし、縦の並びにも何か法則がありそうな気がするんですが、どうでしょう…。
>りょんさんへ
Q20
意見を参考に記事に反映させていただきました。
Q31
そのように具体的に書くと、この問題に限定的と言いますか、<脳内イメージを使う>ことに熟達しないといいますか、そうも書けますが、ここでは敢えて、このままにしています。
Q32
別の記事かこの記事か忘れましたが、そのように書いていた時期があります。(右下が回転→左上が回転)しかし、今の解説の方がスマートなのでこう書いています。また、テンキーを用いた解説を省き、解説を書き直しました。
Q35
記事中の解説に別の表現での解説を加えました。(折り込む→軸)
Q36
ありがうございます。Q36をここまで簡潔に言い表した——あらゆる視点で311,322,321という組み合わせが表れる——は感嘆しました。
Q38
なります。
真ん中の矢印の足元を左側の図形の右下に固定し、矢印の方向へ引っ張ります。すると左側の図形の固定してある右下の点をもとに図形が伸張します。それが右側の図形です。真ん中の×については法則性が定かではないので考えから除外しました。
*縦の並びについて
問題を縦に別けて考えるのなら、<矢印の方向に図形を回転させる>で考えれます。
矢印が一方側なら図形の伸張とみてとれますが、左右にあるなら回転とみてとれます。
左側は左右の反転、真ん中は右斜めに傾けると見れなくもないが考えから除外し、右側は矢印の向きに沿って上下反転する。——と考えられます。
この記事ではなるべく一貫して上段中段下段という横分けの表現を使ってきました。
なので縦分けの解説は入れませんでした。
早々のお返事有難うございます。
また、拙案の一部採用、ありがとうございます。
下記にまた追加案など書きますが、無理にでも解説文の変更を押し付けるという意図ではなく、同じ問題を楽しむ者同士の雑談的な議論程度に考えていただければ幸いです。
Q31
現在の説明でも、この問題に限定的である事はさほど変わりが無いように思えます。
脳内イメージを使う事に熟達しない、というのは「説明を読んだ人が」でしょうか?
確かにそれはあるかもしれません。
結局は、現在のゆゆ様の説明文も、私が書いたコメントも同じことを表しているのですが、左-中央の変化(直線が膨らんで曲線になる)をイメージさせてから中央-右の変化(内側に膨らんだ線が今度は外側に膨らむ)へと移る方が自然であると考えたのと、中段の花のような図形に関して言えば、「中央の図形の左右の辺」と言う表現が、変化するべき線を明確に指し示しているようには思えないので、変化するべき線を明確に指し示しやすい左の図形をすべての起点として説明するべきかと思い、前回のコメントを書きました。
すべての図形は、左上の正方形の4つの辺のうちいくつかを半円状に変形したものと捉えることが出来ますが、説明なしでそれに気が付かない人もいると思いますので、それについての説明の後であれば、「左右の辺」と言う表現の指し示す意図が明確になるとは思います。
これも、読んだ人に頭を使わせるという意味では、親切過ぎなのかもしれませんね。
Q32
これに関しては、どちらがスマートか、と言うより好み、感性的な問題のように思います。
私としては、最初は単に位置のみで判断出来る「右下→左上」の方がシンプルでスマートに思えましたが、少し考えを改めました。
結局、この問題では「右下が90度回転→左上が90度回転」でも「最初に90度回転した斜線と同一線上に並んだ斜線が次に回転」でも解けるので、どちらでもいいですね。
※ちなみに少し気になったのが「重なり合う」は表現として適切ではない気がします。
「水平」も図形の傾きにかかわらず画面上の左右方向を表す言葉ですので、「同一線上に並ぶ」というべきでしょうか。
また、場合によってどちらかの法則のみが正解にたどり着くような出題も可能なので、どちらか一方がよりスマートな思考であるとは言えないように思いました。
たとえば、この問題の下段が下記のように入れ替えられたとします。
/ / / / ( \/ )
/ / / \ ( /\ )
そうすると、最初の回転で、同一線上に並ぶ斜線が存在しないため、正解にたどり着くためには「右下が回転した後に左上が回転する」という説明でなければならなくなります。
逆に、この問題の下段がこのように入れ替えられたとすると、
/ / / / ( /\ )
\ / / / ( // )
この場合は最初に回転する場所が変わっており、「左→中央で最初に回転している斜線と同一線上に並んだ斜線が次の中央→右で回転する」という法則を使わなければならなくなりますね。初見での難易度は若干こちらの方が高いと思います。
Q38について
なるほど、言い換えれば「引っ張ると同時に図形が回転しながら伸長する」という事でしょうか?
右下に固定して~、というのを、最初は平行四辺形歪みのような状態を想像して読んでいましたが、斜めに回転してから引っ張る、あるいは引っ張ると同時に回転するという事ならおっしゃる通りだと思います。
私が先に書いたのは、「上段と同じように」「本当に引っ張るだけなら」正解の形にはならない、という事でしたが、矢印の向きが図形の回転方向も同時に表わしているとすれば合理的ですね。
とすると、これを上段と下段で、一方向矢印の共通の機能として一般化すると、真の機能は「矢印の根元側に底辺が来るように図形を傾け、矢印方向に引っ張って伸ばす」と言えますね。
「図形の上辺をつまんで矢印方向に引っ張る(同時に向きも変わる)」とも言えると思います。
これなら、上段と下段の矢印は全く同じ機能を持っていると言え、一貫性が保たれますね。
次に両方向矢印の意味ですが、私はこれは色の配置のみを逆にする機能と考えていました。
両矢印の機能を回転とすると、左列から、矢印の向きに関係なく常に180度の回転となってしまい、方向に意味が無い事になってしまいます。
それを踏まえて、確実に正解にたどり着け、なおかつ、なるべくツッコミの入らない解説をしようとすると、
——–
前提:左上の図形を起点とし、隣接する矢印の機能によって右または下に向かって図形の変換が行われ、最終的に下段右の図形に至る。中央は無視する。
法則1. 一方向の矢印は、矢印の根元が底辺となるように図形を傾け、矢印方向に引っ張って伸ばす。
法則2. 両方向の矢印は白黒の配置を現在の逆に変更し、図形中の斜めの線の位置も含めた図形の形状には影響しない。
※例えば上段右の図形は矢印の指す左上が白、右下が黒であると言える。よって次(下段右)の図形は左上に相当する箇所に黒が配置されるべきである。
法則1.によるだけでFが唯一の正解として浮上する。色が反転していると考えられる同形のDの可能性もあるが、実際に上段と比較すると、法則2.によりDは否定され、Fが正解となる。
また、仮に法則1.の一方向の矢印の機能に対する理解が不十分でも、法則2.だけを使ってFGHに絞ることが出来る(CDは白黒が逆、ABEは白黒を左上と右下に分けられない)。
この3つのうち、もしHが正解なら、上段と同じようにただまっすぐ上に引っ張っているだけなので、下段中央も上段と同じく単に上向きの矢印となる筈。でもそうではないので、Hの可能性は消える。
Gが正解なら、右上向きの矢印には図形の回転効果しかないことになり、上段の矢印と比較して機能に一貫性がなく、非合理的であるので不適である。
よってやはりFを正解とすることが出来る。
——–
というところで、どうでしょう。
私が悩んでいた点である「同じ形の矢印には論理的に同じ機能があるべき」という命題もクリアしていると思います。
こうしてみると、不正解の選択肢も非常に論理的かつ巧妙に設定されているように思えますね。
>りょんさんへ
雑談的な議論は好きなので、好きというか大抵の人が嫌って避けられる話題で、こちらとしても無用な対立の原因になるので、なるべくはしたくないのですが、したいのならしましょう。
Q31
・より多くの人に伝わるように、表現を変えた法則を追記しました。
・より多くの人に伝わるように、解説に図形変化について追記しました。
Q32
・より多くの人に伝わるように、表現を変えた法則を追記しました。
「水平」と「重なり合う」を別々のものとして切り取ることは「詭弁」ではないでしょうか。「水平に重なり合う」で意味が通じるものを「水平」と「重なり合う」という別々の言葉にして考えられても、主張の裏付けにはなりません。誤った事実です。
「同一線上に並ぶ」でも「水平に重なり合う」でも意味は通じます。文章を読んで想定するイメージは読者の方によります。人それぞれです。この文章で意図するのは、読者の方が「棒が水平に重なりあった状態」を想起させることなので、目的は果たせたものと考えます。
そして、りょんさんの主張はわたしの主張の言い換えであり、私の主張は通るものと考え、両者の議論は議論というよりも言葉選びによる感性の違いであると考えます。
また、コメント中部・下部についてですが、これは自分の主張を通すために創作したデータです。よって主張を補強する効力はないと考えます。
Q38
より多くの人に操作感が伝わるように、「図形の上辺をつまんで矢印方向に引っ張る(同時に向きも変わる)」を解説に追記しました。
【色の反転について】
>両矢印の機能を回転とすると、左列から、矢印の向きに関係なく常に180度の回転となってしまい
とありますが、違います。
”矢印の向きに関係なく常に180度の回転”とはなりません。
なぜなら、矢印には<向き>があるからです。
中段左側の矢印は、水平方向への回転を表していると考えられます。
中段右側の矢印は、斜め方向への回転を表していると考えられます。
このように、問題を縦割りで見たとき、<両矢印は矢印方向へ回転させる>で説明ができます。
りょんさんの主張である、<両矢印は色の反転>では解答であるDは導き出せず、
<両矢印は矢印方向へ回転させる>だと、回転させる際に矢印方向へ向きも変わるため、解答であるDも導き出せます。
また、縦割り横割り統一の法則性を見つけ出そうとする際にも、<両矢印は色の配置のみを逆にする>という機能は不自然に思います。
なぜなら、<両矢印は矢印方向へ回転させる>で説明がつくからです。
それに、矢印の機能である<伸張>。つまり、<図形変化>なのに対し、色の配置のみを逆にするは<彩色変化>であり、<彩色変化>機能は変化の次元が違うように感じます。矢印の数が増えただけで別次元の機能を持たせるのは不自然です。
それならば、<両矢印は矢印方向へ回転させる>としたほうが、同じ<図形変化>なので、矢印が両矢印にパワーアップした感が機能面においてユニバーサルデザイン的に伝わるような気がします。
面倒な議論に長々とお付き合わせしてしまい、恐縮です。
たしかに、このような議論は場が荒れやすいですね。
私としては、お互いの説明や表現の不備を指摘しあう事によって、お互いが個々に作り上げた説明文、表現よりも、さらに優れた解説文や美しい表現が出来上がっていくことが面白いという思いがあるのですが、ともすると否定の応酬になってしまう場合が多々あるのは残念な所です。
この辺で、最後にしたいと思います。
Q38
なるほど、回転させる角度も矢印の方向によって変えるという事ですね。
矢印が両側になったことで、その機能が彩色に関するものになるのは不自然である、と言う主張は全くおっしゃるとおりです。(ただ、肝心の解答はDではなくFです…おそらくただの誤記だと思いますが)
私がしたかったことは、両方向矢印と一方向矢印のそれぞれに、誰もが誤解無くその意味を受け取れるような機能説明をただ一つ付与するという事です。
それさえ実現されていれば、どのような説明でもいいと考えていました。
ただ、配色のみの変化に限るとしたのは、今思えば確かに苦し紛れの妥協であったかもしれません。
縦の系列だけでは一発で正解を導けないというのもその通りです。
おそらく、ゆゆ様の意図する、「両方向矢印の機能は回転であり、矢印の角度によってその回転の角度が変わる」というのは正しく、問題製作者の意図もそうなのだろうと思います。
ただ、それを説明する場合は、どこを基準にどういう回転をするか、なぜそう判断できるのか、誰が読んでも間違いようのない正しさを持った説明が必要であると思います。
しかし、この両矢印の機能の説明について、「水平方向への回転」、「斜め方向への回転」、という表現だけでは、この矢印と説明を合わせて見ても、万人が誤解無く意味を受け取れるほど確定的な意味を持たないように思われます。
既に正解を知っている状態であれば、変化前と変化後の図形を照らし合わせて「なるほど、斜め方向への回転と言う言葉はこういう意味で使っているんだな」と、文意を補完して理解できると思います。しかし、少々いじわるな例ですが、たとえば選択肢の一覧と一方向の矢印がともに隠された状態で「左縦列は左右の両方向を指す矢印があるので、水平方向の回転をしています。右縦列には右下と左上の両方向を指す矢印があるので、斜め方向への回転をしなさい」と言うような言葉で指示した場合、全員が誤解無くFの状態に思い至るとは思えません。
そこで、このような三段論法による推論はどうでしょうか。
・左列では、水平方向の両矢印により図形が180度回転している(事実)。
・ 右列の矢印は、左列の矢印が右回りに45度回転した形となっている(事実)。
・よって右列では、180度の回転に加え、更に右回りに45度回転するのではないか(推測)。
なんだ、言ってることは同じじゃないかと思うかもしれませんが、単純にどの程度多くの人に誤解無く伝わるかと言う基準で表現を見直したものです。
矢印が斜めだから回転も斜め、と言う説明は根拠として弱いですが、「二組の矢印を比較すると、それぞれの形の矢印がともに45度回転していると考えられるから、結果も回転前の矢印の機能に加えて45度回転する」と説明するのは十分に合理的かと思いますが、いかがでしょうか。
この「矢印が回転したから結果も回転する」という単純なルールは一方向の矢印にも適用でき、
・上段では、一方向の矢印によって図形が上に引き伸ばされている(事実)。
・下段の矢印は、上段の矢印が右回りに45度回転した形となっている(事実)。
・よって下段では、上段と同じ変形に加え、更に右回りに45度回転するのではないか(推測)。
と言うことができます。
また、中央の×には矢印を45度回転させる機能があると考えると(今考えると気づいてなかったのが自分でも不思議ですが)、「両方向の矢印は左に135度回転しているとも言える」という意見を明確に否定できますね。
まとめると、
——–
・左縦列の水平方向の両矢印は図形を180度回転させていると考えられる。
・上段の上向き矢印は図形を上に引き伸ばしていると考えられる。
・中央の×は2種類の矢印をともに時計回りに45度回転させていると判断できる。
・回転された各矢印にも、元の機能に加えて結果を45度回転させる効果が付与されると推測する。
上記より導ける正解は縦横どちらでもFのみとなり、推測が正しいと判断できる。
——–
これでどうでしょう。
さて、この記事ではあくまで上中下段での解説にこだわっているという事ですので、無理に中央の×や縦列の両方向矢印を含めた解説を本文に反映させる必要はないかと思っていましたが、今にして思えば、これは縦と横の変化を合わせて初めて完全な合理的説明が可能になる良問だと思いますので、検討の価値はあるのではと思います。
現在は、一方向の矢印のみに関する、同じ事柄を言い換えた3つの表現を並べておられますが、これはコメント欄での経緯を知らずに解説を読まれた方には誤解を与えそうですので、せめて単純にもっとも万人向けと思われる一つの解説に絞られるか、3つの説明が同じ事柄に関する言い換えであることを明示するべきかなと思います。
もし必要なら、私がこれまでのコメントで書いた解説文などに関してはいかなる権利も主張しませんので、どのように改変、組み合わせされても構いません。
「矢印の根元に図形の右下を固定」や、Q32の「水平に重なり合う」という表現についての主張を見ても感じましたが、失礼ながらゆゆ様の選ばれる表現には一部、その意図するところは正しいものの、その文だけを読んで、万人が誤解無く意図したとおりの意味で受け取れるかどうかという点では、やや苦しい場合があるようにお見受けします。
言葉選びの感性の問題であり、論理的な正しさの問題ではないというのも理解できますが、これらの解説に選ぶ表現は、正解を先に提示されずに解説文だけを読んで、誰もが「なるほど、ということは正解は確実に○だな」と思い至るものであるべきと、個人的には考えています。
もちろん、そういう判断基準を採用するべきかどうかも、人によって考えの違うところであると思いますので、誰もがそうしなければならないとは言いません。上記の指摘も重箱の隅をつつくようなものです。
「正解を提示しているのだからこの説明で必要十分、後はご自身でお考え下さい」というスタンスもこの手の問題に挑戦する人に対してはアリだと思います。
>りょんさんへ
りょんさんの文章の言い換え能力——ある文章が人に誤解なく伝わるように言い換える力——文章がスラリとした日本語になるので素晴らしいと思います。
意見を言い合うことで議論に深みが増し、あらたな発展をみせることが面白いと感じるこころも共感します。
”失礼ながらゆゆ様の選ばれる表現には一部、その意図するところは正しいものの、その文だけを読んで、万人が誤解無く意図したとおりの意味で受け取れるかどうかという点では、やや苦しい場合があるようにお見受けします。”
ようやく本心を言ってくれましたね。嬉しいです。
コメントありがとうございました、これをきっかけに記事全文を書き直しました。
この記事は約3年前のものなので文の構成として未熟な部分がありました。
解説の欄を法則性と解説文に別け、可読性を高めました。
ありがとうございました。
Q38
片矢印:矢印の方向に伸張
両矢印:90度回転
さらに上記2つとも矢印が縦方向を向く状態を基準として傾いた角度だけ回転させる
行
左上の図形を上に伸張したもが右上の図形
左下の図形を上に伸張、-45度回転したものが右下の図形
左上の図形を90度回転、さらに90度回転したものが左下の図形
右上の図形を90度回転、さらに45度回転したものが右下の図形
中央の×はQ4の中央にある図形みたいなもので特別な意味はないと思いました。
ダミーさん
コメントありがとうございます。
自分も中央の図形は特別な意味はないと思います。
ただ単に、図全体の整合性を保つために、それが一番美しく収まる記号だからだと思います。
上下は矢印記号で、四隅は白黒の四角なので。
自分の説明よりもダミーさんの説明の方が、わかる人にはわかりやすいと思います。
本文で紹介させてもらいました。
ありがとうございました。
>それが一番美しく収まる記号
IQテストの意味が分かった。
生活環境や過去や未来では答えが変わる可能性がやっぱりあるのだな。
ななしさん
コメントありがとうございます。
これからも示唆のある解説を心がけます。
34の解説が理解できません。
内側と外側(プラスマイナス)で計算式になるのはわかったのですが、黒点の位置に法則性が全くないのにはどうも納得できません。
なにか法則性はないのでしょうか?
ゆうさんへ
納得できない気持ちわかります。
黒点の位置に整合性がないのが妙ですよね。
黒点の位置に法則性はなさそうですが、
プラスマイナスの計算式でない解き方ならば、
黒点の位置に整合性をつくることはできます。
1. 左側の図形を水平方向に180度回転させる。
2. 水平方向に180度回転させた左側の図形を、真ん中の図形と重ね合わせる。
3. 黒丸が重ね合わさった場合、その黒丸を消す。
4. 黒丸が円周を挟んで隣り合った場合、その両方の黒丸を消す。
5. 黒丸が消えたら、真ん中の図形の中で一番下側の黒丸だけを時計回りに15度回転させる。
6. もしも5. の操作で黒丸が消えたなら、もう一度3.から5. の操作を行う。
これでも答えはGになります。
無理矢理につくった法則性なので、複雑です。
いかがでしょうか?
Q36
棒グラフの向きでグループ分けして、各グループ内で棒の長さと色の関係を見るのが分かりやすいと思います。
1. 棒グラフを↑←→のグループに分ける
2. 各グループ内で、一番長い棒は黒濃淡全色ある。
一番短い棒も二番目の棒も全色ある。
絞り込み
1. ←グループ:CDFG
2. 一番長い棒が黒:FG
3. 一番短い棒が淡:F
——–
Q38
これは問題自体が不適切なように思いました。
片矢印の効果は左上→右上で例示され、両矢印の効果は左上↓右下で例示されています。
しかし、斜め矢印の効果が例示されていないので、いかようにも推論(こじつけ)できてしまいそうです。
Aさんへ
ご意見ありがとうございます。
Q36:
行を区切って考えるのではなくて、Q36全体で考えるやり方、スッキリしていてわかりやすいと思います。記事に反映させていただきました。
39問目
Fだと思った〜
たしかに解説を読むとそうだけど…
どの柄も3つ隣り合う
(○○○とか
××
×
とか)
ものがないのでFかなと
選択肢で唯一隣り合ってないし!
既出でしたらすみません
あー見落としてました
やっぱりFではダメですね