目次
非表示
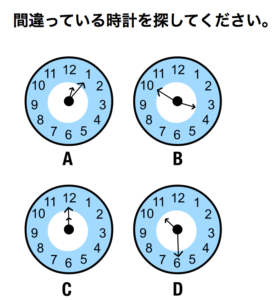
答え B
解説
- 時計の長針は1時間で360度進む。
- 時計の長針は1分で6度進む。
(360度 ÷ 60分 = 6度)|(6度/1分 × 60分 = 360度/1時間) - 時計の短針は12時間で360度進む。
- 時計の短針は1時間で30度進む。(360度÷ 12時間 = 30度)
- 右上の時計は3時50分を示している。
- 長針は6度 × 50分 = 300度
- 短針は30度 × 3時 = 90度
- 長針は300度の位置を示しているから正しい。
- 短針は92度ら辺を示しているから間違っている。
*8.の補足 長針の位置がなぜ300度と判るか
- 時計の短針は1時間で30度進む。
- 時計の短針が10時を示すとき、時計の短針の位置は30度 × 10時 で 300度。
今回は計算しながら答えを割り出しましたが、記憶の中から見たことのない針の型を探り当てれば楽かと思います。
第2問 次に来るのは?

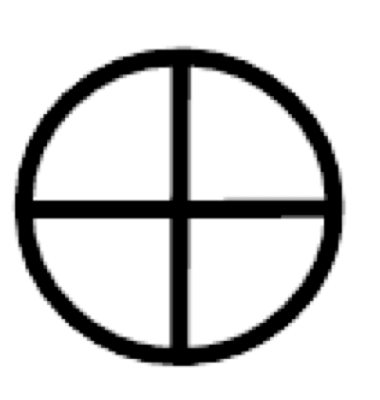
答え C
法則性
- 上段は、丸に縦線を入れた記号が徐々に大きくなっている。
- 中段は、丸に横線を入れた記号が徐々に大きくなっている。
- 下段は、丸に十字線を入れた記号が徐々に大きくなっている
第3問 151、242、333、424 – 次に来るのは?
答え 515
法則性
- 百の位を、プラス1ずつ加算する。
- 十の位を 、マイナス1ずつ加算する。
- 一の位を、プラス1ずつ加算する。
解説
- 151
- 1+1|5−1|1+1 = 242
- 2+1|4−1|2+1 = 333
- 3+1|3−1|3+1 = 424
- 4+1|2−1|4+1 = 515
第4問 次に来るのは?
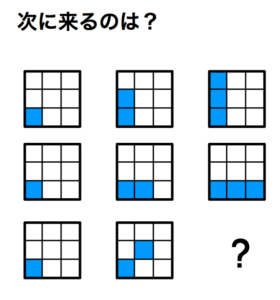
答え D

法則性
- 青マスが左下のマスを起点に1ずつ増えていく。
第5問 次に来るのは?

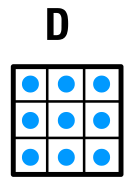
答え D
法則性
- 青マスの数がひとつづつ増えていく。
解説
- 青マス1個→青マス2個→青マス3個→青マス4個→青マス5個→青マス6個→青マス7個→青マス8個→青マス9個
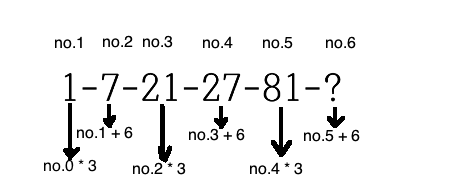
第6問 1、7、21、27、81 – 次に来るのは?
答え 87
法則性
- 奇数個の数字は、直前の数字*3
- 偶数個の数字は、直線の数字+6
解説
- 1 = 0*3
- 7 = 1+6
- 21= 7*3
- 27= 21+6
- 81= 27*3
- ? = 81+6
第7問 Aとつながっているのは?
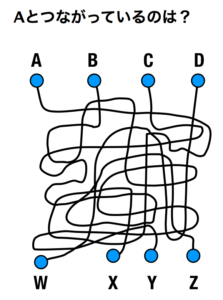
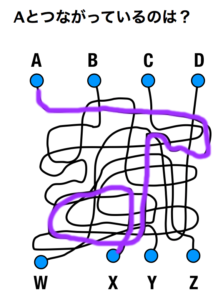
答え X
解説
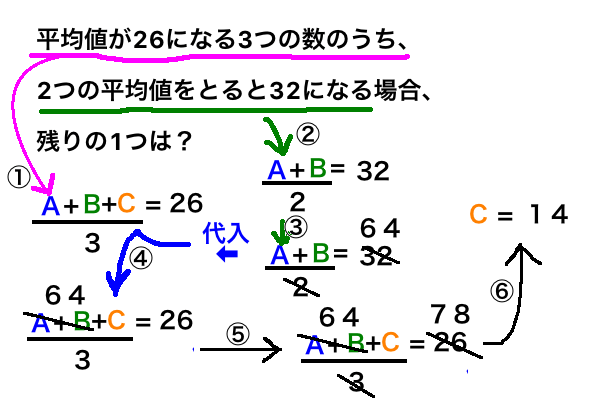
第8問 平均値が26になる3つの数のうち、2つの平均値をとると32になる場合、残りの1つは?
答え 14
解き方
- 愚直に数字を数式で書いていく。
- 平均値が26になる3つの数のうち | ( A+B+C / 3 ) = 26
- 2つの平均値をとると32になる | (A+B)/2 = 32
- 残り一つは?
- ( A+B ) /2 = 32 | A+B = 64
- ( 64+C ) /3 = 26 | 64+C = 78
- C = 14
解説
第9問 空白に入るのは?
答え 98
法則性
- 左列の数字の一の位と十の位の位置を逆さまにして、右列の数字と足すと、真ん中の列の数字となる。
解説
- 69=65 → 56+13
- 63= 14 → 41+22
- ? = 18 → 81+17 = 98
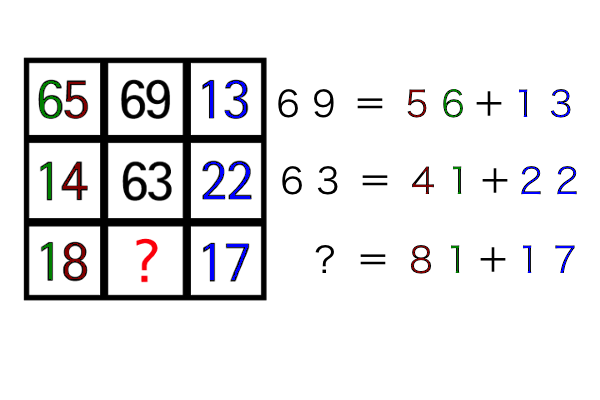
第10問 XからA, B, Cの各点への距離で最も長いのは?
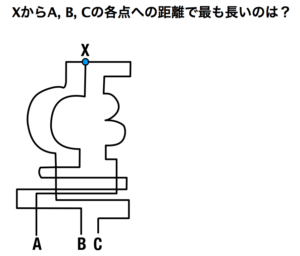
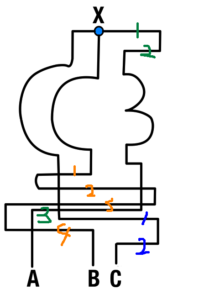
答え B
法則性
- 一番折れ曲がっている回数の多い線が一番長い線となる。
解説
ヒトの小腸は胃に続き大腸へと繋がる消化管である。長さ約6mだが生体内では筋肉の収縮によって3m前後まで縮んでいる。
引用 Wikipedia – https://ja.wikipedia.org/wiki/%E5%B0%8F%E8%85%B8
- 新聞紙を42回折り続けると計算上月に届くのと同じ理論
- 人の小腸の長さは約6m。それが体内に収まっているのは折り畳まれているから。
第11問 仲間ハズレはどれ?

答え 花
法則性
- 花以外は天候の状態を表す
第12問 ある仕事を完了するために、5人がかりで8日かかるとします。2人で同じ仕事をすると何日かかるでしょうか?
答え 20
解説
- 愚直に数字を数式で書いていく。
- ある仕事を完了するために、5人がかりで8日かかる | 5人*8日=40作業量
- 2人で同じ仕事をすると何日かかる? | 40作業量/2人 =20日
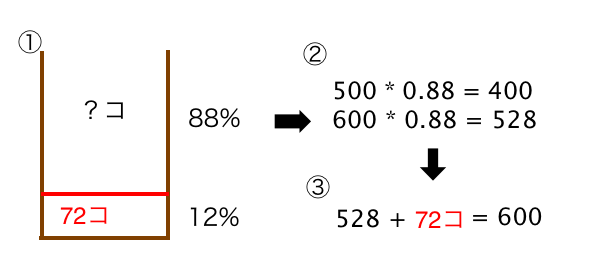
第13問 農園で72個のリンゴが売れました。これが販売に出されたリンゴの総数の12%に当たる場合、その総数はどれでしょうか?
答え 600
解説
- 箱に72個のリンゴがある。
- 箱にあるリンゴは全体の12%
- 残りのリンゴは88% (全体 −12%)
- リンゴの88%を求めたい。|リンゴの残りの数を知りたい。
- 500*88% = 400 … 違う。
- 600*88% = 528 … そうっぽい。
- 88%のリンゴ528個 + 12%のリンゴ72個 = 600個
解説2
- 72 : 12% = x : 88%
- 0.12x = 63.36
- 12x = 6336
- x = 528
- 528 + 72 = 600
解説3
- 72個で12%ならば(72÷12=6)6個で1%ですから、100%は600個
コメント欄「nobara」さんより
全体の数÷いくつ分=1あたりの数
わり算 の 教え方
第14問 間違っている鎖はどれ?
答え C
法則性
- よく見ると鎖が外れている。
図解
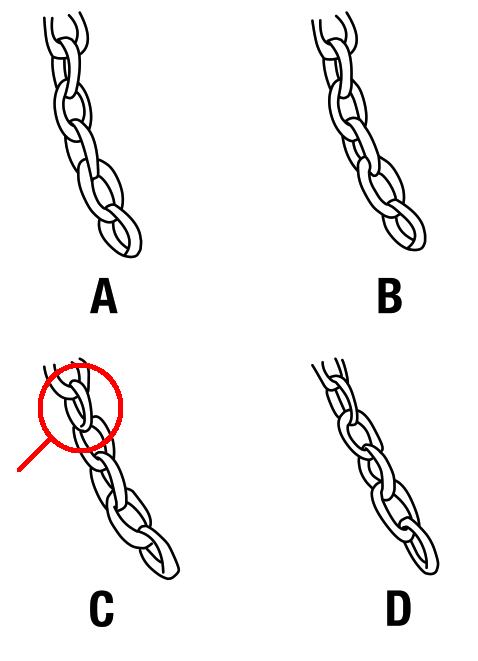
*Aもあやしいが、円柱を真上から見ると円に見えるのと同じ理屈で間違いやすいと思う。
第15問 Xに入るのはどれ?
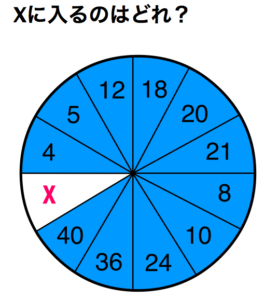
答え 42
法則性
- 真向かえの数字の2倍
解説
- 4*2=10
- 5*2=10
- 12*2=24
- …*2 = …
- 21*2=42
第16問 三角形が一番多いのはどれ?
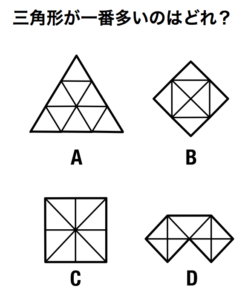
答え D
解説
- 左上の図形:13個
- 右上の図形12個
- 左下の図形:17個
- 右下の図形19個
- 左上の図形を例に考えます。
- 一辺が最小の三角形から探していきます。
- 上段では、一辺が1の三角形が1個
- 中段では、一辺が1の三角形が3個
- 下段では、一辺が1の三角形が5個
- 上中段の中にある三角形の数は1個
- 中下段の中にある三角形の数は2個
- 上中下段の中にある三角形の数は1個
- 合計して13個(1+3+5 +1+2 +1)
図解
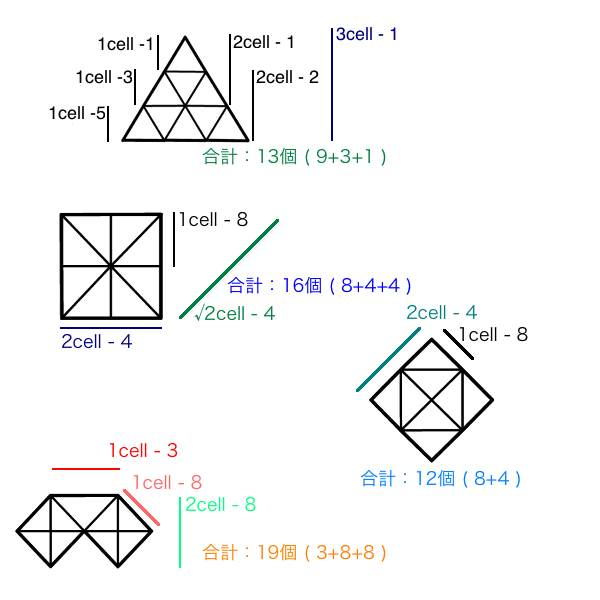
第17問 空欄に当てはまるのはどれ?

答え C
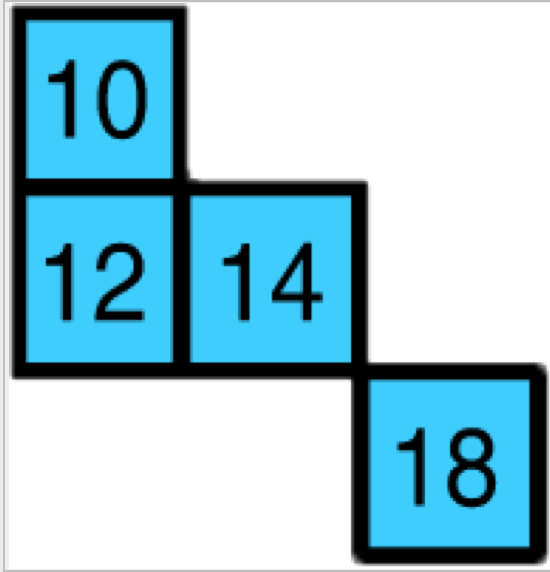
法則性
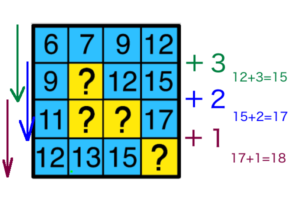
- 2段目は1段目の数値+3
- 3段目は2段目の数値+2
- 4段目は3段目の数値+1
- 10(7+3)
- 12(10+2)
- 14(12+2)
- 18(17+1)
解説
第18問 Xに入るのはどれ?
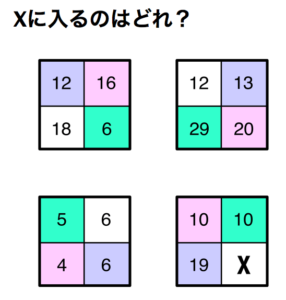
答え 14
法則性
- 各色のマスの数値を合計すると50になる。
解説
- 緑色のマスの合計は50 | 6+29+5+10=50
- 薄ピンク色のマスの合計は50 | 16+20+4+10=50
- 薄紫のマスの合計は50 | 12+13+6+19=50
- 白色のマスの合計は50 | 18+12+6+X=50 | X=14
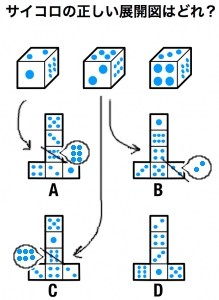
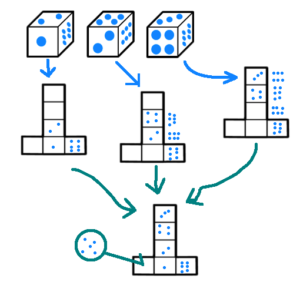
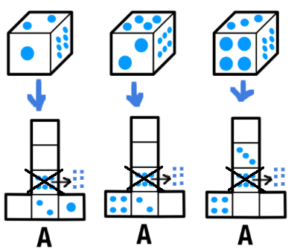
第19問 サイコロの正しい展開図はどれ?
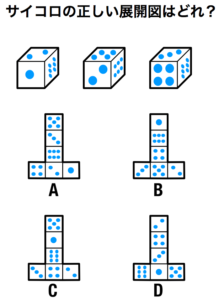
答え D
解説
- 「二」「三」「六」には縦向きと横向きがある。
- 縦横の向きに気をつけて展開する。
- 「A」「B」「C」は展開すると、縦横の辻褄が合わなくなる。
第20問 青い箱は3kg、白い箱は2kgの重さがあります。間違っているのはどれ?
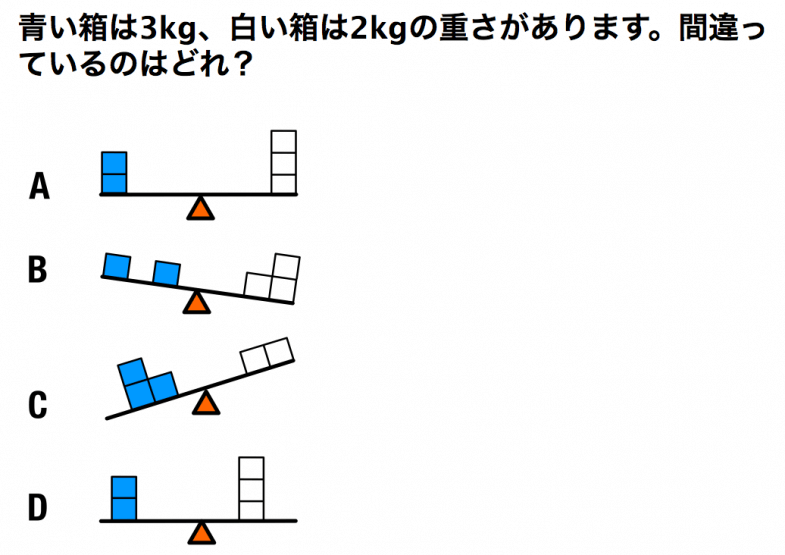
答え D
解説
- A:3番目*2個*3kg = 3番目*3個*2kg
→ 18kg = 18kg 正しい。 - B:3番目*1個*3kg+1番目*1個*3kg < 3番目*2個*2kg+2番目*1個*2kg
→(9+3)<(12+4)→ 12kg <16kg 正しい。 - C:2番目*2個*3kg+1番目*1個*3kg > 3番目*1個*2kg+2番目*1個*2kg
→(12+3)>(6+4)→ 15kg >10kg 正しい。 - D:3番目*2個*3kg = 2番目*3個*2kg
→18=12 → 18kg =12kg 正しくない。
おわりに
以上、全問正解するとこんな感じになります。
以上、IQトライアングルテスト(2016年版)の答えと解説でした!
ありがとうございました。

サイコロの問題で、AとDの違いが分からなくなってしまいました。
上に6、下に5を置いたときに、側面が、1→2→4→3となるような。。。
うーん。
ばたこさんへ
Q19を「A」にしてスコアがどうなるか試してみました。
スコアは「180-200-200」になりました。
よくよく展開図を確認してください。
「二」「三」「六」には向きがあります。
たぶんそれが「A」が不正解になる原因かと思います。
PS.
Q19を更新したので合わせて確認してください。
第13問の解説ですが、72個で12%ならば(72÷12=6)6個で1%ですから、100%は600個というものではどうでしょうか?
第17問の法則性として、私は横方向に+1 +2 +3 という点に注目しましたが、縦方向にも法則性があったんですね。
第9問は解けませんでした。左の数字の位を入れ替えるという視点はなかなか気づきにくいですね。左右の数字の内側どうし、外側どうしを足すと考えたとしても、なぜ内側の数字を十の位にするのか必然性が見つかりませんし…。
第19問 サイコロの展開図、頭の中で図形を回転させるのはなかなか難しかったです。
解説ありがとうございました。
nobara さん
コメントありがとうございます。
問題9.
これは問題製作者よりもnobara さんの方が賢く、問題製作者が気づかない整合性に気づいてしまうからでは。
問題13.
ありがとうございます。記事に反映させて頂きます。助かります。
問題17.
私も最初は横方向で解きました。この問題は別の記事で解説していて、違いを出す為に縦割りの解法を書いた気がします。
問題19.
頭の中で図形を回転させるのは難しいですよね。
これが出来ると、思考操作に自由が利くはずです。まだまだ訓練中です。