
目次
非表示
2015年IQテスト答え一覧と解説
第1問 仲間はずれはどれですか?
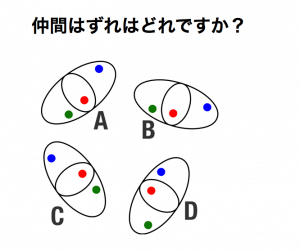
答え D
法則性
- 赤点を中心に回転させると、Dだけ違う画像。 ABCは3つとも同じ画像
第2問
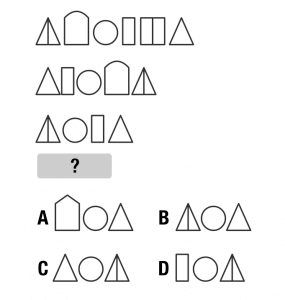
答え C
法則性
- 右から2個目の図形を消して、◯を軸にして左右反転させると下の画像になる
第3問
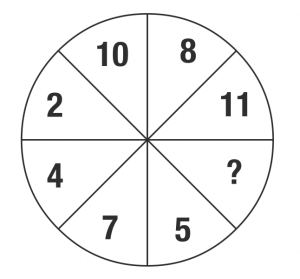
答え 13
法則性
- 向かい合う数字を足すと15になる
解説
- 10 + 5 = 15
- 8 + 7 = 15
- 11 + 4 = 15
- ? + 2 = 15
第4問 1、8、2、7、3、6、4… 次の数字は?

答え 5
法則性その1
- n= 1 , 8 , 2 , 7 , 3 , 6 , 4 …
- n番目とn+1番目の数字の差が7から1づつ減っていく
- 1 – 8 = 7
- 8 – 2 = 6
- 2 – 7 = 5
- 7 – 3 = 4
- 6 – 3 = 3
- 4 – 6 = 2
- ? – 4 = 1
- ? = 1
法則性その2
- 一つ飛ばしで「 1 」を足し算するグループと、引き算するグループに分ける。
- 1 → 2 → 3 → 4 → …
- 8 → 7 → 6 → 5
図解
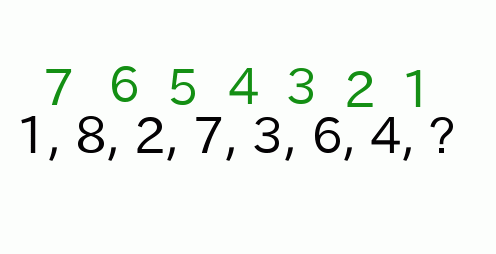
解説
- 1 – 8 = 7
- 8 – 2 = 6
- 2 – 7 = 5
- 7 – 3 = 4
- 3 – 6 = 3
- 6 -4 = 2
- 4 – ? = 1
- ? = 5
法則性その2
- 81、73、63、54・・・
解説その2
- 1、8、2、7、3、6、4…を2つずつ区切ると、81、72、63、54・・・となり九九の9の段の降順と一致する。
参考
第5問
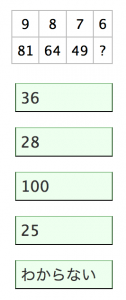
答え 36
法則性
- 上の数字の累乗は下の数字
解説
- 9 * 9 = 81
- 8 * 8 = 64
- 7 * 7 = 49
- 6 * 6 = 36
第6問
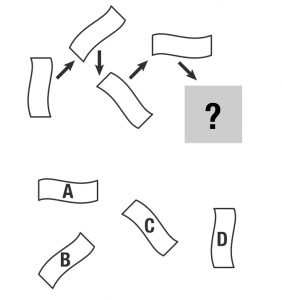
答え A
法則性1
- 時計回りに傾く角度が45→90→135→180と変化していく。
参考
- コメント欄「あ」さんより
法則性2
- 時計回りに傾く角度が45度ずつ増えていく。(45→90→135→180)
図解2
- 3番目を時計回りに135度回すことがイメージしずらかったら、反時計回りに45度回してみてください。
- この図形は点対称な図形です。180度回転させても、360度回転させても同じ図形になります。
第7問 仲間はずれの数字は?

答え 941327
法則性
- 数列を2桁づつ3つに区切る。(681422 を 68 14 22)
- 左側2桁を足すと真ん中の数字になる
- 左側の一の位と真ん中の数字を足すと右側の数字になる
解説
- 681422 → 68 14 22, 6+8 = 14, 8+14 = 22
- 751217 → 75 12 17, 7+5 = 12, 5+12 = 17
- 941327 → 94 13 27, 9+4 = 13, 4+13 = 17, 17≠27
- 831114 → 83 11 14, 8+3 = 11, 3+11 = 14
- 691524 → 69 15 24, 6+9 =15, 9+15 = 24
注釈
この選択肢の中で、「751217」だけが素数です。しかし、問題製作者の方はそのことに気づいていないようです。問7以外の回答を「わからない」にし、問7で「751217」を選択しても得点に加算されませんでした。コメント欄のdonさんからの指摘により発覚しました。
第8問

答え 5
法則性
- 数字の1〜9が一回づつ使われている
図解

解説
- 上側の数列:4, 9, 13, 5, 86, 2, 7 → 123456789
- 左側の数列:4, 82, 79, 6, 35, 1 → 123456789
- 右側の数列:7, 9, 24, 63, 18, ? → 1234 6789
- 下側の数列:1, 6, 37, 8, 49, 2, ? → 1234 6789
- 二桁の数字を一桁の数字に分解する。
- たとえば「13」は”1”と”3”
- 「86」は”8”と”6”。
- 上側の数列「4, 9, 13, 5, 86, 2, 7」は数字の1〜9が一回づつ使われている。
- 左側の数列「4, 82, 79, 6, 35, 1」は数字の1〜9が一回づつ使われている。
法則性2
- 二桁の数字を一桁の数字に分解後の各一列・各一行の総和が45となる。
解説2
- 上横一行: 4 + 9 + 1 + 3 + 5 + 8 + 6 + 2 + 7 = 45
- 左縦一列: 4 + 8 + 2 + 7 + 9 + 6 + 3 + 5 + 1 = 45
- 右横一列: 7 + 9 + 2 + 6 + 3 + 1 + 8 + ? = 40 , ? =5
- 下横一行: 1 + 6 + 3 + 7 + 8 + 4 + 9 + 2 + ? = 40, ?=5
第9問
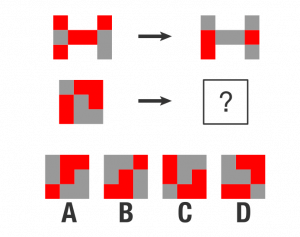
答え B
法則性
- 左側の画像を反転させ、右側の画像と重ね合わせると、灰色は赤く染まる。
- 左側の画像を水平方向に反転させ、色も赤色→灰色と反転させると、右側の画像になる。
- 左側の画像を左右反転させ、色も赤から灰色へ換える。
第10問
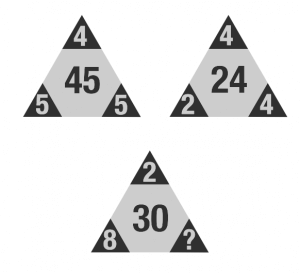
答え 3
法則性1
- (上の数字 + 左の数字) * 右の数字 = 真ん中の数字
解説1
- ( 4 + 5 ) * 5 = 9 * 5 = 45
- ( 4 + 2 ) * 4 = 6 * 4 = 24
- ( 2 + 8 ) * 3 = 3 * 10 = 30
法則性2
- 一番小さな数字を頂点とする
- 底辺の左右の数字をかける = A
- 頂点の数字 * 底辺の右側の数字 = B
- A + B は 真ん中の数字になる
解説2
- ( 5 * 5 ) + ( 4 * 5 ) = 25 + 20 = 45
- ( 4 * 4 ) + ( 2 * 4 ) = 16 + 8 = 24
- ( 8 * 3 ) + ( 2 * 3 ) = 24 + 6 = 30
第11問
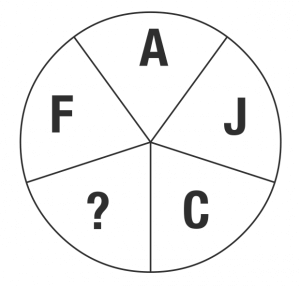

答え O
法則性
- Aを起点に右回りで、一つ飛ばしのアルファベットとの差が1ずつ増えている
図解
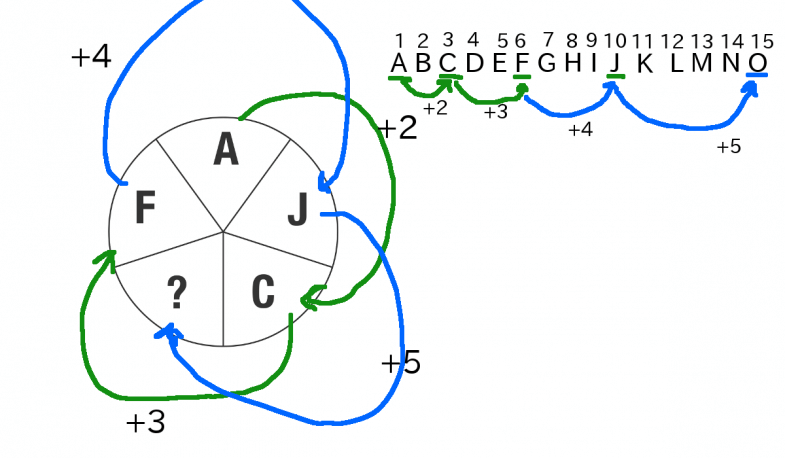
解説
- アルファベットのAから順番に番号を振る。(A=1,B=2,C=3,D=4,E=5,F=6,G=7,H=8,I=9,J=10, … 0=15, …)
- Aを起点に一つ飛ばしでアルファベットに振った数字を見ていく(A→C→F→J→?)
- アルファベットを番号を振った数字に換えると。(1→3→6→10→?)
- (1→3→6→10→?)の差は、2→3→4→?。
- このことから、飛ぶごとに1ずつ飛ぶ数字が増えていくことがわかる
- なので、次のアルファベットは+5飛びと推測できる
- ? は 15番目のアルファベットなので
- 答えは O = 15
第12問
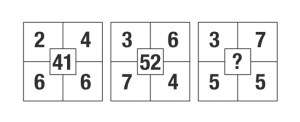

答え 75
法則性
- 左上右上右下 ÷ 左下 = 真ん中
解説
- 246 ÷ 6 = 41
- 364 ÷ 7 = 52
- 375 ÷ 5 = 75
参考
- コメント欄「ミルココ」さんより
法則性
- 左側の2つの数字を掛け合わせる、右側の2つの数字を掛け合わせる
- 掛け合わせた数字を、十の位と一の位で足し算する
- 大きい方から小さい方を引いた値が、真ん中の数字を同じように引いた値と同じになる
解説
- 2 * 6 =12 / 4 * 6 = 24
- 1 + 2 = 3 / 2 + 4 = 6
- 6 – 3 = 3 / 4 – 1 = 3 , 3 = 3
- 3 * 5 = 15 / 7 * 5 = 35
- 1 + 5 = 6 / 3 + 5 = 8
- 8 – 6 = 2 / ? = 2
- 36 → 3 / 48→ 4 /75→ 2 /50 → 5 /47 → 3
参考
- コメント欄「jiffy」さんより
第13問 仲間はずれはどれですか?
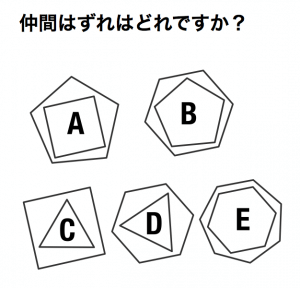
答え D
法則性
- 外側の角数 – 内側の角数 = 1
解説
- A: 5 – 4 = 1
- B: 6 -5 = 1
- C: 4 -3 = 1
- D: 5 – 3 = 2
- E: 7 – 6 = 1
第14問

答え B
法則性
- 左側の図形と真ん中の図形を重ね合わせ、重複している線が右側の図形となる
第15問 2,0,3,2,6,7,14,… 次の数字は?

答え 20
法則性
- n番目 + (n+1)番目の数字の和がフィボナッチ数列順になっている。
解説
- 2 + 0 , 0 + 3 , 3 + 2 , 2 + 6 , 6 + 7 , 7 + 14
- 2 , 3 , 5 , 8 , 13 , 21
- 2 + 3 = 5
- 3 + 5 = 8
- 8 + 13 = 21
- 13 + 21 = 34
- 34 – 14 = 20
図解

第16問
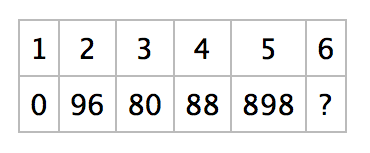
答え 888
法則性
- 下段の数字にある穴の数の合計が、上の数。
解説
- 1→0
- 2→0
- 3→0
- 4→1
- 5→0
- 6→1
- 7→0
- 8→2
- 9→1
- 0→0
第17問

答え 7
法則性
- n = 1, 2, 3, 4, 5, 6, …
- 上段 + 中段 + n = 下段
解説
- 5 + 0 + 1 = 6
- 2 + 9 + 2 = 13
- 3 + 4 + 3 = 10
- 8 + 5 + 4 = 17
- 7 + 8 + 5 = 20
- 6 + ? + 6 = 19
第18問 仲間はずれはどれですか?

答え D
法則性
- Dの記号の画数だけ、1、1、3、4。他の記号の画数は1、2、3、4
解説
- A:2、1、3、4 → 1234
- B:4、2、1、3 → 1234
- C:2、4、3、1 → 1234
- D:1、1、3、4 → 1134
おわりに
もしも全問正解するとこのような画面になります。
以上!IQtest 2015 ver の解答と解説でした!
ありがとうございました。

たくさんの解説記事いつも参考になります。
第6問は
時計回りに傾く角度が45→90→135→180と変化していく。
だと思います。
>あさん
なるほど!そういうことでしたか!
たすかりました。
ありがとうございます。
はじめまして。
2015年IQテストがおもしろかったので、
こちらのサイトも閲覧させていただきました。
第12問目の法則性が不明とのことですが、
偶然かもしれないものの、
なんとか計算して正解しましたので、
そのときの計算法を記述させていただきます。
法則性
上下の数字を掛けて、
右側の答えから左側の答えを引いたうえで、
一桁の場合はそのまま、
二桁の場合は十の位と一の位を足すと、
真ん中の数字の十の位から一の位を引いた数になります。
解説
左側
4*6-2*6=12
1+2=3
4-1=3
真ん中
6*4-3*7=3
5-2=3
右側
7*5-3*5=20
2+0=2
?
なので、
答えは 75(7-5=2)になります。
亦、
第8問目の解答法にはびっくりしました。
愚生は、
全数字を解体すると、
一列の総和が45になり、
右側と下側の和が40なので、
答えが5だとおもっていました。
このサイトのように、
もっとスマートに解答できるのですね。
感動しました。
第12問目も、
解法が複雑すぎるので、
もっとスマートな計算法があるかもしれませんが、
一応、
正解したので、
参考程度におつたえしておきます。
> jiffy さん
jiffyさん。はじめまして。
これで解説が揃いました。ありがとうございます。
第12問めですが、この解法が一番スマートかと思います。
正方形を十字に区切って真ん中に回答が置かれている図形と、
解き方のイメージ(引っ張ってひねって下ろす感じ)が一致するので。
これ以上はないように思います。
第8問目はたしかに総和の解法ですね。
解説に加えさせていただきます。
追記:
と、思いましたが、解説を書き終わった後にjiffyさんの解法と違いがないか確かめたところ、解釈に違いがありました。十の位と一の位を足し合わせる順番が違っても解けるようです。
第六問
なのですが答えがAと言う事になると360度回転してる事になりませんか?
>いときん さん
たしかに、360度回転させてもおなじ画像になります。
なぜなら、Aは点対称の画像だからです。
点対称の画像とは、中心点を中心に180度回転させても同じになる画像のことを言います。
たとえば、「□」や「◯」、「◇」がそうです。
ここのサイトが詳しいです(http://www.geisya.or.jp/~mwm48961/math3/tentaisyo.html)
納得できなければ、
いまからAの画像を操作するので、次のことを脳内でイメージしてください。
1. Aの画像左下のトンがっている部分を、反時計回りで、180度回転させてください。右上にきます。
2. Aの画像右上のトンがっている部分を、反時計回りで、180度回転させてください。左下にきます。
3. Aの画像左上の丸みのある部分を、反時計回りで、180度回転させてください。右上にきます。
4. Aの画像右下の丸みのある部分を、反時計回りで、180度回転させてください。左下にきます。
(回転させるときは、Aの画像の中心点を中心に回転させてください。)
いじょうのことから、Aの画像は180度回転しても、Aの画像と同じであることが分かるかと思います。
点対称の図形は180度回転させても、360度回転させても同じ図形になるので、そのことが混乱の原因かと思います。自分はそうでした。
>>ゆゆさん
ご返信有難うございます。
私の認識力不足の所為なのか未だに理解が出来ずにいます。
Aが点対称の画像と言う事ですが
>>ゆゆさん
すいません↑の返信は誤って投稿してしまいました。
よく考えて見て理解が出来ました。
知らずの内に図を立体視していたのでこの様な混乱が起こって
しまっていたようです。
ご回答有難うございました。
>いときんさん
どういたしまして!ありがとう!よかったです!
ゆゆさん、こんにちは。第7問なのですが、ゆゆさんの解説はすごく納得しました。そこでふと思ったのですが「仲間ハズレの選択肢を選ぶ」という設問条件の範囲内に於いて751217も答えになるのではないでしょうか。751217だけ唯一、数字記号の中に空間の部屋が存在する(6,8,4,9のような)数字が含まれていない選択肢だと思いました。そういった意味で、751217は仲間ハズレなのではないのかなあと思いました。
>橋本さんへ
こんにちは。橋本さん。お気づかいありがとうございます。
たしかに751217だけ空間の部屋が存在しない数字ですね。
その視点から見たら、751217もあながち間違えでもないし、答えにもなりうると思いました。
数字を空間の部屋という観点から見る視点が独創的で素晴らしいとおもいます。
問4、9の掛け算に見えてしまい、そのまま5と回答してしまいましたw
なんか変な当て方ですよね笑
>がんさんへ
おおすごい、たしかに81、72、63、54ですね。。。
第12問ですが、「真ん中の数字は四角の中のどの数字でも割り切れない」と考えると47が答えになってしまうので、正直悪問でしょう……
> かめさんへ
・・・そういった視点もありますね
3問目は別の法則性もありますね。
10を基準に時計回り、2を基準に反時計周りで?まで隣の差をとる。
時計回り:2,3
反時計周り:2,3,2
基準となる10と2の差は8
?が13であれば、8,2,3,2,8の差ループが完成する。
スパちゃんさん
なるほど。シュッとしてて周りからジワジワ攻める感じがいいですね!
ループで確認ができるのも美しくていいですよね。
簡単な問12の計算方法
左上右上右下÷左下=真ん中
例:246÷6=41
ミルココさん
感服しました。
コメントを記事に反映しました。
わからなかった問題がいくつかあったので解説すごくうれしいです!
第十八問を三角形がないものはどれかでいくとAも答えになっちゃいますね
さらにBも下記のようにいくと答えにできます・・・
交点と頂点の数と交点にも頂点にもなってなく止まってるところの数を比較する。
たとえば×なら
交点が1個、交点にも頂点にもなってなく止まってるところが4個で
△なら頂点が3個、交点にも頂点にもなってなく止まってるところが0個となります
そしてそれぞれの交点+頂点の和と交点でも頂点でもなく止まってるところの和、どちらが多いか考えると
A→交点でも頂点でもなく止まってるところ
B→交点と頂点
C→交点でも頂点でもなく止まってるところ
D→交点でも頂点でもなく止まってるところ
となりBだけ仲間はずれに・・・!
(ちなみにCだけ線対称にも点対称にもならない図形が含まれてるという意味ではCも仲間はずれになります、すなわちどれを選んでも正かry)
また第三問ですが、こじつければ「7」が答えにできました(選択肢ないですけど)
やり方なのですが 八等分されてるのを 上半分 下半分 右半分 左半分 にわけそれぞれの総和をもとめ
上半分の総和×下半分の総和=右半分の総和×左半分の総和となるような値を求めるというやり方で
上半分の総和=31
下半分の総和=16+?
右半分の総和=24+?
左半分の総和=23
となり方程式を解くと?=7が答えになっちゃいます笑
タバサッチさん
18問はたしかに、D以外にも仲間はずれにできますね。
第6問ですけれど、問題の矢印の向きが→,→,→,→の様に同じ向きではなく、わざわざ右上、真下、右上、右斜め下になっています。矢印が→,→,→,→なら45度ずつ回転でもいいのでしょうけれど。問題ではなぜわざわざ矢印の向きを変えているんでしょうか?
WadaPeach さん
コメントありがとうございます。
言われてみたら、わざわざ矢印の方向が変わっているのは変ですね。
結論を先に申しますと、
出題者の方は問題の難易度を上げる為に、わざと矢印の向きを変えたのだと思います。
この問題の法則性は「時計回りに傾く角度が45度ずつ増えていく」ですが、
問題の矢印の向きを→,→,→,→の様に同じ向きに揃えると、
この問題の法則性を簡単に見破ることができると思います。
「45度→90度→135度→180度」のような、
単純な角度の加算問題になるからです。
このIQテストは2015年バージョンでして、同じ出題者の方は2014年バージョンも制作されております。
2015年バージョンは冒頭に、昨年のテストよりも難しくしましたとの旨が書かれています。
これらを鑑みると、
出題者の方は単純に、
為に、問題でわざわざ矢印の向きを変えたのだと思います。
考え方は間違ってたけど答えは偶然あってた
第2問
左右の端が交互
第4,6問
一つおきに見た
第12問
6☓4=24 6☓1=6→41
7☓5=35 7☓2=14→52
5☓7=35 5☓5=25→75
ほかは解説してもらったのとだいたい同じ考え方でやった。
第16問は分からなかったので解説でスッキリした。
ながどん さん
コメントありがとうございます!
お役に立てたようでよかったです!
( )+( )=( )
( )+【 】=【 】
【 】+【 】=( )
問題
( )と【 】に入る言葉を漢字2文字でそれぞれ答えなさい
いさおさんへ
():零時
【】:六時
答えは751217だけ素数じゃないですか?
※941327は137で割り切れます。
don さんへ
コメントありがとうございます。
おっしゃる通り、選択肢の中だと751217だけ素数です。
ですので、答えは751217でも良いと思います。
しかし、問題製作者の方はそのことに気づいていないようです。
なぜなら問7で「751217」を選択すると得点に加算されないからです。
解説文に注釈を付け加えました。コメントありがとうございました。